南极大陆面积约为1400×10[4]km[2],冰盖和冰架面积占了总面积的97.6%,是全球现代冰川总面积的86%。南极冰盖的平均厚度为2450m,冰储量达2937.8×10[4]km[3],占地球表面淡水资源的85%[1]。南极冰盖记录了远古时期的环境变化和气候变化,对南极冰盖的研究能够获取这些信息,从中探寻环境和气候变化的规律,解释现代环境和气候的成因,进而预测未来的环境和气候变化,对人类社会的发展具有重要的意义。玛丽伯德地(MarieByrdLand,73°S—85°S,100°W—150°W)是西南极洲的一部分,位于罗斯冰架、罗斯海以及太平洋南部,山地复杂,是南极洲最偏远和最难进入的陆地之一。玛丽伯德地基岩暴露较少,大部分被南极西部的冰盖掩盖,该地区的深入研究对其附近的冰海相互作用、环境域分析和生态研究有重要的意义[2]。

地表粗糙度是冰盖或冰川表面的重要特征,是边界层气象学的标志,是地表高度测量精度的重要限制因素[3,4]。冰盖表面坡度和粗糙度主要受基岩地形、冰流、冰厚、风和质量平衡的影响[5,6],反映了冰盖表面的起伏程度,冰盖表面的坡度分布是冰盖从远古时期冰盖表面演化过程的一个重要标志[7],定量表征冰盖表面粗糙度具有重要意义。国内外学者针对冰盖表面粗糙度进行了很多相关研究,可以通过卫星遥感图像、机载激光测高、多角度成像光谱仪等分析冰盖表面粗糙度[8,9,10]。利用雷达回波散射信号也可以分析冰盖表面的粗糙度。1987年Ogilvy[8]总结了波散射分析自然表面粗糙度的方法,并提出波散射分析自然表面粗糙度在某些地方尚有不足。1998年VanderVeen等[9]利用高分辨率机载激光测高法确定格陵兰中部的冰盖表面粗糙度,论证了利用机载激光测高法描述极地冰盖表面统计特征的可行性。2002年Nolin等[10]利用多角度成像光谱仪研究格陵兰冰盖西部等地区冰盖和海冰表面的角特征,并根据角特征的成像方式分析冰盖表面、海冰表面的粗糙度特性。2011年Cathles等[11]利用辐射传输的数值模型,研究了太阳辐射驱动的消融与格陵兰冰盖表面粗糙度增长之间的反馈。Grima等[12]根据机载探冰雷达回波散射信号的统计特性分析了西南极Thwaites冰川的表面粗糙度。

本文采用1998年12月—1999年1月由德克萨斯地球物理研究所(UTIG)航空地球物理研究支持办公室(SOAR)对南极洲玛丽伯德西部区域空中调查获得的表面高程数据,分析了利用均方根高度、自相关长度、有效坡度、均方根坡度以及绝对坡度等粗糙度表征方法在该地区的适用性并对该区域的表面粗糙度分布进行了研究。均方根高度、自相关长度、均方根坡度和绝对坡度实际上仅考虑了表面在单一方向上的变化;有效坡度则同时考虑表面在垂直和水平方向上的变化,分析表明,有效坡度能够更好地表征研究区域的表面粗糙度。最后本文给出了玛丽伯德地西部区域表面的有效坡度分布并进行了简要分析。

1、数据和方法

1.1数据

本文采用美国冰雪数据中心提供的1998年12月—1999年1月西南极玛丽伯德地西部区域冰盖表面高程数据,该数据由德克萨斯大学地球物理研究所(UTIG)航空地球物理研究支持办公室(SOAR)获得[13],该区域所在位置和雷达测线以及相应的表面高程如图1所示。该次调查使用了一架装载雷达和激光测高仪的双水獭飞机,在1998年12月—1999年1月共进行了64次航空调查,并根据雷达回波测得冰盖表面、基底高程数据。研究区域面积约460×360km[2],包括罗斯冰架东部的谢里斯海岸、爱德华七世半岛的大部分地区、苏兹伯格冰架和福特山脉。大部分调查区域的飞行轨道间距为5.3km或10.6km。

图1玛丽伯德地西部表面高程图.

左下角插图中的红框表示研究区域在南极洲的位置

数据通过航线飞行时间的先后顺序存储,本研究按照飞机航线提取冰盖表面高程数据。在每一条航线中,每100个样本点组成一个样本空间,根据每一样本点的经纬度数据得到样本点之间的距离,每一样本空间的尺度在1.5km左右。将每一样本空间的表面高程数据减去相应样本尺度上表面高程数据的平均值,将得到的新的数据作为研究的样本空间。

1.2数据预处理

由于玛丽伯德地山地崎岖和测量的误差,原始表面高程数据集中存在多组异常值,首先我们对各个航次的表面高程数据进行筛选,根据玛丽伯德地实际高程分布状况去除明显异常值,然后将处理后的数据用于之后的研究,数据处理过程如图2所示。

图2数据预处理

1.3研究方法

国内外学者采用了多种定量表征表面粗糙度参数的方法,包括均方根高度、自相关长度、有效坡度、均方根坡度以及绝对坡度等[8,9,10,11,12],这些方法可以归为两类:仅考虑表面在垂直方向或水平方向上的变化以及同时考虑表面在两个方向上的变化。本文分别通过两类方法对研究区域的表面高程数据进行了计算,并分析了它们的可靠性。

1.3.1均方根高度

均方根(RMS)高度是最常见且最容易获得的参数,它是关于高度平均值的标准差。通常的计算方式[4]如下所示。

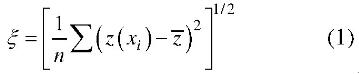
其中,n是样空间中样本点的数量,z(xi)是在位置处样本点的表面高度,是该样本空间所有样本点的平均表面高度。均方根高度可以反映样本空间在垂直方向的变化。

1.3.2自相关长度

样本空间的自相关函数是样本空间与自身在被某一阶跃或延迟抵消时的标准化协方差[4],根据定义,当延迟为0时,自相关函数等于1。

自相关长度为:

通常定义为使归一化后的相关值降低到1/e(37%)所需要的距离或延迟。光滑表面通常具有较大的自相关长度,而粗糙表面具有较低的自相关长度值。自相关长度反映了样本空间在水平方向上的变化。

1.3.3有效坡度

在雷达散射模型中,通常将表面粗糙度定义为均方根高度与自相关长度的比值[14]。在很多情况下,这个比值被混淆为均方根坡度,为了减轻混淆,Campbell和Garvin[15]给出有效坡度的定义:

有效坡度通常以度为单位:

1.3.4均方根坡度

均方根坡度也是常见的表征粗糙度的参数,即均方根偏差除以步长

这里的均方根偏差定义为延迟或者步长分隔点之间的高度均方根差:

均方根坡度通常以度为单位:

1.3.5绝对坡度

部分研究学者认为,均方根坡度不能很好地代表剖面的真实特征,因为离散的点和较长坡度的频率分布会使均方根坡度趋向较高的值,为了减轻个别高的或错误的斜坡影响,可以使用绝对坡度[16]:

绝对坡度通常以度为单位:

2、结果与分析

2.1均方根高度以及自相关长度

通过公式(1)可以得到均方根高度,通过公式(2)和(3)可以得到自相关长度,它们分别描述的是表面的垂直变化和水平变化。我们计算了研究区域的均方根高度和自相关长度,为分析其用于表征表面粗糙度的可靠性,选取航线Wx-X11a中均方根高度相同的三组样本空间a、b和c以及自相关长度相同的三个样本空间d、e和f进行分析。它们的均方根高度、自相关长度以及相应的有效坡度值如表1和表2所示,相应的表面高程变化如图3所示。从表1和表2中可以看到,若单以均方根高度或自相关长度来表征表面粗糙度,则a、b、c三个样本空间的表面粗糙度相同,d、e、f三个样本空间的表面粗糙度也相同。然而从图3a可以看到,a、b、c样本空间中c具有较小的粗糙度,单一使用均方根高度并不能完全体现研究区域的表面粗糙度。三者的自相关长度(水平变化)依次增大,有效坡度依次减小,则更加符合图3a所显示的结果。从图3b可以看到,d、e、f三个样本空间中f更加平坦,具有更小的粗糙度,单一使用自相关长度并不能完全体现研究区域的表面粗糙度,而三者的均方根高度以及有效坡度依次减小,更加符合图3b所示的结果。

表1样本空间(a,b,c)的均方根高度、自相关长度以及有效坡度值

表2样本空间(d,e,f)的均方根高度、自相关长度以及有效坡度值

通过以上两组的比较,我们可以发现单一的水平(自相关长度)和垂直方向(均方根高度)的粗糙度不能全面表征研究区域的表面粗糙度,垂直变化相同的样本空间之间的水平变化可能并不相同,反之亦然,因而综合垂直方向和水平方向的变化来表征研究区域的表面粗糙度可能是个更好的选择。

2.2有效坡度

随机选取一条航线(Wx-X11a)分析研究区域冰盖表面的有效坡度,该航线起点(80.077°S,151.1443°W)至终点(79.0988°S,147.2493°W)总长约140km。图4为该航线上的表面高程,我们可以看出航线起点位置延伸60km(第一阶段)的冰盖表面起伏较为平缓;在60—100km位置(第二阶段)冰盖表面呈上升趋势,此后100—140km(第三阶段)表面高程下降又上升。

分别从三个阶段中各任意提取一个样本空间,分别记为(1)、(2)和(3),它们在航线上的位置如图4所示。表3列出了3个随机样本空间的均方根高度、自相关长度和有效坡度值。从表3中可以看到,样本空间(2)的有效坡度值(1.3840°)最大,样本空间(1)的有效坡度值(0.0926°)最小。图5为3个随机样本空间的表面高程,从中可以明显看到样本空间(1)的表面整体平坦,粗糙度较小;样本空间(2)表面呈锯齿状,并且整体呈上升趋势,粗糙度较大;样本空间(3)表面前期起伏不大,后面呈平缓上升趋势,总体粗糙度介于(1)和(2)之间。结合表3和图5可知,表面的有效坡度值能够较好地表征表面的粗糙度,有效坡度越大,冰盖表面粗糙度越大。

图3样本空间高程分布变化.

图4航线(Wx-X11a)表面高程图.

(1)(2)(3)为随机选择的用于研究的样本空间位置

2.3均方根坡度和绝对坡度

我们计算上述同一条航线(Wx-X11a)的均方根坡度和绝对坡度的分布情况,航线(Wx-X11a)的每个样本点之间的平均距离为15m左右,因此均方根坡度和绝对坡度的步长((35)x)取15m,通过计算我们得到航线(Wx-X11a)中90个样本空间的均方根坡度和绝对坡度分布(图6a、b)。从图6a、b中可以看出航线Wx-X11a的均方根坡度和绝对坡度的分布是一致的,数值的差异是计算方式导致的;而他们与有效坡度分布(图6c)存在明显的差异。为分析用均方根坡度、绝对坡度和有效坡度表征航线(Wx-X11a)表面粗糙度的可靠性,我们从航线Wx-X11a中选取三个样本空间x、y和z,它们的位置及对应的三种粗糙度值如图6所示,它们的表面高程如图7所示。它们的均方根坡度、绝对坡度和有效坡度结果如表4所示。

表3航线Wx-X11a随机样本空间(1)(2)(3)的均方根高度、自相关长度和有效坡度值

图5航线Wx-X11a中随机样本空间(1)、(2)和(3)的表面高程

通过比较样本空间x、y和z的表面高程分布(图7),我们可以发现样本空间x的表面高程起伏变化最小,样本空间y的表面高程起伏变化最大,从表4中我们可以看出有效坡度的大小变化更加符合x、y和z三个样本空间表面变化。由于均方根坡度和绝对坡度的计算中,水平间隔(35)x是固定不变的,不能反映不同样本空间在水平方向上的变化特征,而本文中研究区域的横向变化较为复杂,因而在本研究中均方根坡度和绝对坡度不能够较好地表征表面粗糙度;在有效坡度的计算中,自相关长度数值依据样本空间水平变化的特征发生改变,能够更好地反映不同样本空间的水平变化特征,因此我们认为,相较于均方根坡度和绝对坡度,在本研究中采用有效坡度作为衡量冰盖表面粗糙度的依据更为可靠。

图6航线Wx-X11a的三个坡度分布图.a)均方根坡度;b)绝对坡度;c)有效坡度

图7样本空间x,y,z的表面高程分布

2.4玛丽伯德地西部区域有效坡度分布

利用上文的方法计算了研究区域的整体有效坡度值,为便于分析,图8中分别给出了有效坡度值小于10°和有效坡度值大于10°的位置。从图8中可以看到,研究区域98%左右的表面有效坡度值小于10°,有效坡度在10°以上的位置主要分布在靠近海岸地区。

表4航线Wx-X11a中样本空间x、y、z的均方根坡度、绝对坡度、有效坡度值

结合bedmap2的高程数据对本研究中粗糙度(有效坡度)的空间分布进行分析。图9a至图9e给出了罗斯冰架附近(图8中A点)、福特山脉附近(图8中B点)、爱德华七世半岛附近(图8中C点)、图8中样本空间(D)以及(E)的表面高程图以及对应的有效坡度值。为保证表面高程起伏一致,图9a至图9e的左图为样本空间的整体剖面图,右图为表面高程放大图,水平方向长度1.2km,垂直方向间隔100m。

图8玛丽伯德地西部区域的有效坡度分布

图9样本空间表面高程图及对应的有效坡度.(a)—(e)分别对应样本空间A—E

从图8左图我们可以看出罗斯冰架附近有效坡度值分布在3°以下,我们在罗斯冰架附近选取样本空间A(78.7560°S,150.9328°W到78.7489°S,150.9802°W),该样本空间的有效坡度值为0.764°,从样本空间A的表面高程图(图9a)我们可以发现样本空间A的表面高程缓慢上升且无起伏,具有较低的粗糙度。从图8右图中可以看出在福特山脉附近出现有效坡度急剧增大的情况,在福特山脉选取样本空间B(77.002°S,144.8973°W到77.0107°S,144.8370°W),该样本空间的有效坡度值为16.6307°,由图9b中可以看出样本空间B的冰盖覆盖面较小,高程持续增大且中间略有起伏,具有较大的粗糙度。爱德华七世半岛有效坡度主要分布在1°下,极个别样本空间的有效坡度超过1°,我们选取样本空间C(78.0752°S,155.3992°W到78.0838°S,155.4375°W),该样本空间有效坡度值为6.7629°,根据图9c我们可以看出该样本空间高程持续增大且无起伏,其变化幅度高于A小于B,粗糙度在两者之间。相较于样本空间B(福特山脉附近),该样本空间更平坦,其附近是海岸地区,有效坡度值都大于1°。

样本空间D(76.877°S,139.4512°W到76.8651°S,139.4262°W)附近的高程都在1000m以上,其位置如图8所示,高程剖面图如图9d所示,样本空间D的高程呈上升趋势,高程变化在20m左右,其对应的有效坡度为2.9188°。样本空间E(80.1449°S,146.6963°W到80.1551°S,146.7348°W)附近的表面高程主要在800m以下,其位置如图8所示,高程剖面图如图9e所示,样本空间E的高程也呈上升趋势,高程变化在16m左右,比样本空间D的高程起伏变化略小,而样本空间E的有效坡度(3.004°)却略大于样本空间D(2.9188°),这是因为样本空间E的自相关长度(293.703m)要比样本空间D的自相关长度(325.6885m)小。

综上所述,样本空间A所在的罗斯冰架区域有效坡度值分布差异较小,均在3°以下;而样本空间B所在的福特山脉一带,由于冰雪覆盖较少,雪冰表面高程受岩石地形影响较大,具有较大的有效坡度值。最大有效坡度值(39.9736°)的样本空间位置为(77.8017°S,154.8420°W到77.7928°S,154.8050°W)。样本空间C所在的爱德华七世半岛的大部分区域的有效坡度值在1°以下,最小有效坡度值(0.0126°)的样本空间位置为(79.5331°S,153.5161°W到79.5427°S,153.5611°W),该样本空间表面平坦,起伏变化平缓,属冰原区域;样本空间D和E所在区域雪冰积累较厚,表面高程受基岩的影响较小,有效坡度值整体不高,差异不大。

3、结论与展望

本文研究了玛丽伯德地西部以及罗斯冰架东部的谢里斯海岸等地的冰盖表面粗糙度分布。研究利用1998年12月—1999年1月航空调查获得的研究区域的冰盖表面高程数据,讨论了使用均方根高度、自相关长度、均方根坡度、绝对坡度以及有效坡度来表征表面粗糙度的可靠性,并给出了研究区域的粗糙度分布。按雷达测线将数据分成若干个样本空间,每个样本空间尺度为1.5km左右,最终每一个粗糙度参数代表一个样本空间。通过研究发现:由于只考虑了表面在单一方向的变化,仅使用均方根高度(垂直方向的变化)或自相关长度(水平方向的变化)不能很好地表征表面的粗糙度;均方根坡度和绝对坡度采用了固定的水平间隔,因而实际上也难以描述水平方向变化复杂的地形。本研究中结合均方根高度和自相关长度,考虑表面在垂直和水平方向的变化,使用有效坡度(均方根高度/自相关长度)能够有效地表征表面的粗糙度。本研究对整个研究区域的高程数据进行计算,给出了研究区域的表面有效坡度分布。研究区域98%左右的表面有效坡度值小于10°,最小有效坡度为0.0126°。有效坡度在10°以上的位置主要分布在靠近海岸地区,爱德华七世半岛、谢里斯海岸附近的部分地区有效坡度值达到30°以上,最大有效坡度为39.9736°。在雪冰积累较厚的区域,雪冰的表面高程受基岩的影响较小,表面的有效坡度值整体不高,且差异较小,而在雪冰积累较薄的福特山脉区域,表面的有效坡度受到岩石表面的影响较大,具有较大的有效坡度值。

冰盖表面粗糙度不仅跟表面地形相关,同时也跟风和积累率等其他因素相互影响,冰芯数据以及实测积累率数据能够从一定程度上反映表面粗糙度的影响。由于缺乏相关实测数据,本文仅对玛丽伯德地西部区域冰盖表面粗糙度进行了研究,随着南极科考的不断深入,未来将进一步研究该区域的表面粗糙度与积累率等的相互关系。

参考文献:

[6]晁强,窦银科,孙波,等.南极内陆冰盖表面地貌特征监测系统设计及应用分析[J].极地研究,2016,28(4):548-554.

董洪伟,杨树瑚,徐佳鑫,张云,韩彦岭,洪中华.基于航空高程的玛丽伯德地西部地区表面粗糙度的研究[J].极地研究,2020,32(02):202-211.

基金:国家自然科学基金(41506213,41376178,41401489)资助.