
摘要:运用ANSYS Workbench软件建立不同弯曲半径的弯管模型,分析了弯曲半径对所受流体压力以及内部流速分布的影响,得到了弯曲半径和管道入口压强对固有频率和整体变形的关系。结果表明:弯曲半径对流速分布影响显著,弯头处内侧流速大,外侧流速小;弯曲半径对弯头后段内壁压力影响显著;弯头处内侧受压小,外侧受压大;弯曲半径对整体变形的影响较小,而管道入口压强对整体变形的影响大;管道2、3阶固有频率随着弯曲半径的增大有下降趋势,随着弯曲半径的增大4阶固有频率增大明显。
 加入收藏
加入收藏
随着输流管道系统广泛的运用在生物医学、石油化工、船舶海洋等多个领域,管道系统的安全性与稳定性的保障变得越发重要。流固耦合力学主要研究由于结构场和流场的变形导致的流体与结构之间的相互作用,即流体的非定常流动导致结构变形,而结构变形反过来又会影响到流体的流动状态。这种两相介质之间的相互作用现象常出现在各种工程领域,拥有广阔的应用背景[1]。
自1950年,H.Ashley等[2]首次提出流固耦合力学后,国内外的众多学者在此方面进行了深入的研究,郭长青等[3]研究了输流管道系统的振动和稳定性问题。刘凤友[4]运用传递矩阵法研究了流体流经圆弧曲管的振动稳定性问题。李艳华[5]参考Tenteralli的建模思想,对弯管进行整体建模及求解。喻萌等[6]运用ANSYS软件对不同约束条件下的管道系统进行了模态分析并提供了管道优化设计和管道维护指导。
输流弯管与直管道相比,弯管的情况更为复杂。首先,由于弯管流道强制流体改变运动方向,因而弯管处的流体压力波会在弯管壁上作用不平衡的轴向和横向压力;其次,结构的轴向和横向运动也不再互相独立,而是耦合在一起,并产生结合部耦合[7]。赵宁[8]运用ANSYS软件建立弯管流固耦合有限元模型,研究了压力、流速和管径三参数对管道系统振动频率的影响。俞树荣[9]以流固耦合理论为基础,运用ANSYS对比分析了单向流固耦合受力和双向流固耦合受力。A.S.Tijsseling[10]在文章中提到管道系统流固耦合的主要形式为摩擦耦合、泊松耦合、结合部耦合、Bourdon耦合、波流耦合和波波耦合。
本文运用ANSYSWorkbench软件中联合AN-SYS-CFX软件求解FSI的建模方法。在一般情况下,根据物理场耦合程度的不同将耦合场分为弱耦合场、强耦合场、超强耦合场。为了满足在不同耦合场中计算要求,在ANSYSWorkbench中提供了三种建模方法[11,11]。1)单向耦合,先求解两个场其中之一,然后将所求结果作为另一个场的边界条件或以外荷载的形式加载上去。2)双向耦合,将流场方程与结构方程依次独立求解,然后将每个时间步长所求的结果以荷载的形式加到对方的场中。3)完全耦合,将流场方程与结构方程放入同一个巨大的矩阵中求解,求解过程非常困难,同时也不适用与ANSYS-CFXCoupling,本文不考虑完全耦合的情况。
运用ANSYSWorkbench软件对管道建模,进行仿真模拟计算,研究了弯曲半径对所受流体压力、变形以及内部流速分布的影响,并通过模态分析讨论弯曲半径和管道入口压强对管道固有频率的影响[12]。
1、有限元模型建立
如图1所示,为单向耦合的建模求解流程图[13],在Geometry模块中创建几何模型,使用Mesh模块划分网格,两个物理场之间的载荷在耦合见界面上可实现自动传递而并不需要拥有匹配的单元节点,但节点的不匹配会直接影响到求解精度。因此建议在ICEM中同时创建管道和流场的单元,分别将划分好的单元格导入各自的软件,然后进入FluidFlow(CFX)模块定义流体属性,并求解计算,最后将计算结果以荷载的形式添加到StaticStructural模块中,并在其中设置约束等外界条件,最后进行求解,得到管道在耦合状态下的应力变形图及流体的流速迹线图。而双向耦合是将流体域和固体域的计算结果按照一定长的时间步相互传递,然后继续进行运算,得出结论。
图1求解流程图
下文将以弯曲半径为32mm的弯管单向耦合为例详细说明仿真步骤。
1)采用ANSYS-Geometry模块建模,如图2所示,设某输流弯管直径d=64mm,壁厚h=2mm,几何尺寸L1=L2=500mm。管道材料为结构钢,其密度为7850kg/m3,弹性模量为200GPa,泊松比为0.3,管道内的流体介质为水,其温度为22℃,密度为998.2kg/m3,流体黏度γ为0.001kg/(m·s)。
图2弯管模型
2)采用ANSYS-Mesh进行网格划分,如图3所示,分别划分流体域和固体域网格,并在流固交界面设置加密的网格膨胀层,综合考虑计算时间和精度后,尽量使用六面体单元,并设置单位网格尺寸为3mm。
图3管道单元格划分
3)划分网格后分别在流体域和固体域模块中进行前处理。在流体前处理中首先定义流体的区域并将流体材料设置为水,不考虑热能传递和湍流的影响,然后添加荷载,将入口总压设置为3×101.325kPa,5×101.325kPa,8×101.325kPa,12×101.325kPa,出口设置为1×101.325kPa。固体结构前处理时,将管道材料设置为结构钢,两端设置为固定约束并定义流固接触面。
4)在FluidFlow(CFX)模块中进行流体域运算,得到流体流速迹线图和流体压力场分布云图,并将运算结果以荷载的形式通过流固接触面传递到管道结构上。
在StaticStructural模块中进行固体域运算,得到管道整体变形、最大主应变和最大主应力。
2、静态耦合分析
本文建立弯曲半径分别为32mm、96mm、160mm、224mm、288mm、352mm的弯管模型,分别对设置入口总压为3×101.325kPa,5×101.325kPa,8×101.325kPa,12×101.325kPa,耦合计算得到流体流速迹线图、管道压力云图和管道变形数据,分析了管道弯曲半径和管道入口压强对这些量的影响。
1)流体流速迹线图
图4为入口总压设置为12×101.325kPa时各管道流体流速迹线图,管道上端为入口,下端为出口。随着迹线的颜色由蓝色逐渐转变为红色,表示流体流速的增加。
由图4可见,随着管道弯曲半径的增大,管道内流体流速显著增加;管道弯头处内侧流速最大,外侧流速最小;流体流经弯头前后的迹线比较发现弯头后的流速略大于弯头前,但是弯头后的迹线不如弯头前稳定。
2)管道压力云图
图5为入口总压设置为12×101.325kPa时各管道压力云图,管道上端为入口,下端为出口。随着管道颜色由蓝色逐渐转变为红色,表示管道内壁受到压力增加。
由图5可见,随着管道弯曲半径的增大,管道内壁整体受压不断减小,而弯头后段管道内壁受压减小显著;管道弯头处内侧受压最小,外侧受压最大。
对比管道压力云图和流速迹线图发现随着流速的增加,流体对管道内壁的压力减小,管道弯曲半径对控制管道内流体流速和管道内壁压力有显著的作用。
3)管道变形图
绘制弯曲半径为32mm、96mm、160mm、224mm、288mm、352mm的弯管在入口压力为3×101.325kPa,5×101.325kPa,8×101.325kPa,12×101.325kPa下的整体变形图、主应变图、主应力图。
图4不同弯曲半径管道迹线图
图5不同弯曲半径管道压力云图
整体变形Utotal是一个标量,变形结果仅和移动自由度有关,Ux、Uy、Uz表示管道在x、y、z方向上的变形量,它由下式决定
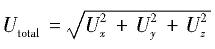
主应变是指应变椭球体主轴方向的应变。主应力为物体内任一点剪应力为零的截面上的正应力。
由图6可见,管道弯曲半径的变化对整体变形的影响较小,而压强对总变形的影响显著。
由图7可见,压强越大管道最大主应变越大;最大主应变随着管道弯曲半径的增加呈现先降后增的趋势;但当管道弯曲半径较小或较大时,最大主应变受弯曲半径的影响较大,而弯曲半径适中时最大主应变几乎不受弯曲半径的影响。
由图8可见,随着压强增大管道最大主应力增大;而随着管道弯曲半径的增大,管道最大主应力的变化并不明显。
3、耦合振动特性分析
弯管弯头处为耦合振动中最敏感的部位[14],为进一步研究不同弯曲半径管道的振动性能差异,分别对弯曲半径为32mm、96mm、160mm、224mm、288mm、352mm的弯管进行模态分析,得到如图9所示的前6阶的固有频率变化曲线。
图6整体变形图
图7最大主应变图
图8最大主应力图
由图9可见,随着管道弯曲半径的增加,管道1、5、6阶固有频率稳步增大,而2、3阶管道固有频率随着弯曲半径的增大呈现先降后升的趋势;4阶管道固有频率在弯曲半径较小时较2、3阶固有频率差别不大,但随着弯曲半径的增大固有频率增大明显,在弯曲半径较大时趋于稳定。
图9不同弯曲半径管道固有频率
故为了避免共振对管道结构的影响[15],对于低频振动的情况,应使用弯曲半径较大的弯管,对于高频振动的情况,应使用弯曲半径较小的弯管。
4、结论
1)随着管道弯曲半径的增大,管道内流体流速显著增加;管道弯头处内侧流速最大,外侧流速最小;弯头后的流速略大于弯头前,但是弯头后的迹线不如弯头前稳定。
2)随着弯曲半径的增大,管道内壁整体受压不断减小,而弯头后段管道内壁受压减小显著;管道弯头处内侧受压最小,外侧受压最大。
3)管道弯曲半径的变化对整体变形的影响很小,而压强对总变形的影响显著。压强越大管道最大主应变越大;最大主应变随着管道弯曲半径的增加呈现先降后增的趋势。压强越大管道最大主应力越大;管道最大主应力随着管道弯曲半径的增大变化并不明显。
4)随着管道弯曲半径的增大,管道1、5、6阶固有频率稳步增大;2、3阶管道固有频率随着弯曲半径的增大呈现先降后升的趋势;4阶管道固有频率随着弯曲半径的增大固有频率增大明显。
在工程运用中,弯管弯头处为耦合振动中最敏感的部位,管道在满足实际用途的条件下选择合适的弯曲半径,对工程有重要的参考价值。
参考文献:
[1]王涛.基于ANSYSWorkbench的输液管道振动特性分析和振动控制的研究[D].石家庄:河北科技大学,2011.
[3]郭长青.输流管道与轴向流中板状结构的流致振动与稳定性[D].北京:清华大学,2010.
[4]刘凤友.输流曲管的振动稳定性分析[J].强度与环境,1991(1):9-17.
[5]李艳华.考虑流固耦合的管路系统振动噪声及特性研究[D].哈尔滨:哈尔滨工程大学,2011.
[7]李帅军.管路系统流固耦合动力学计算及特性分析[D].哈尔滨:哈尔滨工程大学,2015.
[8]赵宁.基于Workbench的流固耦合作用下弯管的振动分析[J].辽宁化工,2017,46(8):795-796;799.
[9]俞树荣,马璐,余龙.弯曲输流管道流固耦合动力特性分析[J].噪声与振动控制,2015,35(4):43-47.
[11]窦益华,于凯强,杨向同,等.输流弯管流固耦合振动有限元分析[J].机械设计与制造工程,2017,46(2):18-21.
[11]于瀛.基于ANSYSWorkbench的管道系统流固耦合振动特性分析[D].沈阳:东北大学,2017.
[14]叶红玲.输流弯管的流固耦合模态分析及参数影响研究[C]//中国力学学会计算力学专业委员会.中国计算力学大会2014暨第三届钱令希计算力学奖颁奖大会论文集.中国力学学会计算力学专业委员会:中国力学学会,2014:579-583.
[15]夏永胜,张成龙.基于ANSYSWorkbench的液压管道流固耦合振动分析[J].流体传动与控制,2017(3):38-41;57.
谌冉曦,韩天宇,郭长青,刘颖.基于Workbench的输流弯管流固耦合分析[J].南华大学学报(自然科学版),2020,34(02):69-73+81-82.
基金:国家自然科学基金项目(51678286).
分享:

专业导论课程是各个工科专业都要开设的一门必修课程,旨在介绍本专业的研究对象、发展方向、关键技术及课程体系,通过该门课程的教学让学生对专业有一个总体上的了解,并为后续的专业课学习提供系统性指导,同时也需要培养学生树立投身于祖国工业和国防建设的伟大理想,在专业导论课的教学方面,多位教师学者都提出了很多教学改革思路[1,2,3,4,5]。
2024-07-17
在网络信息发达、繁杂的时代背景下,青年大学生极易接触到不良的思潮和价值观,存在急功近利的价值取向,缺乏家国情怀,集体责任感以及坚定的社会主义人生理想信念。大学生在校期间的绝大多数时间是在非思政类课程学习中度过。习近平总书记在全国高校思想政治工作会议上强调指出“要用好课堂教学这个主渠道。
2020-12-15
腐蚀是普遍存在于国民经济和生产生活中的重要破坏因素,学者们针对材料腐蚀现象进行了众多研究,其中,静态环境下的腐蚀研究已较为丰富。在流动体系中,流体对材料表面及腐蚀产物膜的力学冲刷作用、对腐蚀性离子的传质促进作用以及对界面反应过程的影响使得流动环境下的腐蚀问题更加严重和复杂。
2020-12-03
在核反应堆中,控制棒驱动机构是反应堆控制和保护系统中重要的伺服机构,控制棒驱动机构是驱动控制棒组件运动、实现准确调节反应堆内反应性变化的重要部件,控制棒驱动机构具有实现反应堆启动、提升功率、保持功率、负荷跟踪、正常停堆和紧急事故停堆等重要的安全功能。
2020-11-27
腐蚀是普遍存在于国民经济和生产生活中的重要破坏因素,学者们针对材料腐蚀现象进行了众多研究,其中,静态环境下的腐蚀研究已较为丰富。在流动体系中,流体对材料表面及腐蚀产物膜的力学冲刷作用、对腐蚀性离子的传质促进作用以及对界面反应过程的影响使得流动环境下的腐蚀问题更加严重和复杂。
2020-11-17
房间内污染物来源包括:煤气泄漏、一氧化碳泄漏、室内装修后残留的甲醛等污染物。其中煤气和天然气、CO等污染物通过管道或者开关未关闭泄露至空间中,而室内装修残留物则主要为家具或者地板等使用的材料超出规定指标而不断残留在房间中。本文主要采用CFD的方法进行结构合理性的验证。
2020-11-17
为研究一种高减压比组合式空气减压阀的流场特征,基于计算流体动力学(CFD)方法,建立减压阀数值计算模型,针对两级阀体特征参数组合的典型工况进行仿真计算,研究减压阀流场参数分布,分析柱阀间隙和引气位置对流动状态和减压比影响。计算结果表明,组合式减压阀流场状态复杂,第一级柱阀间隙对于流动损失和局部参数分布有重要影响,两级阀分别通过总压损失和流速变化实现减压过程,通过合理的特征参数组合可获得较大减压比及其调节范围。
2020-11-16
气体在液体中的运动广泛存在于自然界和工程领域中,如发动机水下排气、水下爆炸引起的气泡运动、石油开采.其中的动力学过程在一个多世纪以来一直受到人们的关注[1,2].数值模拟是研究气体在液体中运动的一种有效方法[3,4].由于液体与气体之间的密度比一般远大于重液体与轻液体之间的密度比,所以气液相界面的捕捉一直是数值模拟的重点与难点.
2020-08-10
理论和实践证明,环量控制[1]方法可以通过产生射流在后缘形成Coanda效应[2]来改变环量,从而产生高升力[3]。国内外一些学者针对环量控制参数的影响都进行了研究:Englar[3]、Liu等[4]经研究得出在小攻角、小动量系数下环量控制可产生较大升力的结论;张艳华等[5]通过计算流体力学数值仿真方法(CFD)研究了动量系数和攻角对NASA超临界翼型的升阻特性和附面层分离特性的影响规律。
2020-08-10
流体力学是研究流体在静止和运动状态下的运动规律及流体与固壁相互作用力的一门学科,在机械、能源、汽车、化工、航空、航天等诸多领域有着极广泛的应用[1]。该课程是力学、机械等专业本科生的专业基础课程。由于其涉及数学、物理、力学等内容,概念多,公式推导繁琐,理论性强,实际应用广,对学生综合利用知识的要求较高,是普遍公认的教师难教、学生难学的课程之一[2]。
2020-08-10
人气:8097

人气:7758

人气:6590

人气:6027

人气:4809
我要评论

期刊名称:力学学报
期刊人气:2858
主管单位:中国科学院
主办单位:中国科学院力学研究所
出版地方:北京
专业分类:科学
国际刊号:0459-1879
国内刊号:11-2062/O3
邮发代号: 2-814
创刊时间:1957年
发行周期:双月刊
期刊开本:大16开
见刊时间:一年半以上


影响因子:0.963

影响因子:1.730

影响因子:0.542

影响因子:0.744

影响因子:1.028
您的论文已提交,我们会尽快联系您,请耐心等待!
你的密码已发送到您的邮箱,请查看!