首页 >
论文范文 >
自然科学论文 >
数学论文 >
拓扑论文 >
浅谈微积分和线性代数课程间的联系
摘要：本文通过Lagrange中值定理的行列式法证明、三角形面积与行列式的关系、二次型函数对应的矩阵和函数的线性无关四个问题，试图建立线性代数和微积分间的联系，在实际教学中发现二者相辅相成，相互促进，二者的相互渗透，调动了学生的学习积极性，有利于学生整体感认识的建立。
加入收藏
目前微积分和线性代数属于2门独立的课程，一般是分开讲授的。微积分侧重于讲授极限、微分学及积分学；线性代数注重矩阵及应用。陕西理工大学的微积分（下册）和线性代数同在大一第2学期开设，在给同一个班级讲授微积分的同时讲授线性代数，深刻体会到这2门课程联系紧密，相互交融。尤其是多元函数部分，诸如多元函数的泰勒展开、极值的判定、梯度、二阶偏导数矩阵和坐标转换的雅克比矩阵等，这些内容事实上都是对矩阵的应用。学生在学习一元函数微积分后，明确了导数的几何意义是函数在该点处切线的斜率，因此在学完行列式的定义后，自然会思考行列式的几何意义是什么，以及多元函数与矩阵之间是否有关系等问题。本文试图建立微积分与线性代数之间的一些联系，以引起更多大学数学教师对此类问题的关注。
1、三角形的面积与行列式的关系
设(fx)表示从A到B的曲线，且(fx)在[ab],上连续，P是曲线上任一点（见图１）。考虑三角形
的面积
与行列式
之间的关系。
结论:
，即
面积等于行列式(Fx)取绝对值再乘以
.
证明:设P到底边AB的距离为d，则三角形
的面积
可以表
示为
，这里
直线AB的方程为
，化简得
，利用点
到直线的距离公式，得
，
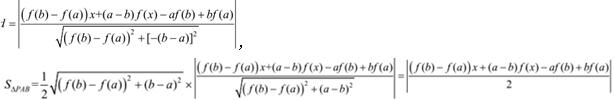由于
所以
证毕.
这里相当于利用三点的坐标，构造了一个行列式，研究了该行列式与对应三角形面积之间的关系。行列式的几何意义也不限于此，也可以用体积来描述行列式的几何意义[1]。
2、Lagrange中值定理的行列式法证明
微积分教材中都是采用Rolle定理来证明Lagrange中值定理，通过构造辅助函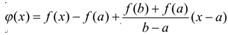
进行证明。本文利用行列式函数
来证明Lagrange中值定理。
引理:考虑行列式
,这里
连续可微，
则
引理的证明可以采用行列式的展开计算证出。
定理（Lagrange中值定理）设函数(fx)满足条件：（1）在闭区间[ab],上连续；（2）在开区间(ab),可导。则至少存在一点
使得
证明构造辅助函数
，则(Fx)满足Rolle定理的条件，即(Fx)在闭区间[ab],上连续，开区间(ab),可导，且F(a)=F(b)=0.于是对()Fx而言，至少存在一点
使
证毕。
Lagrange中值定理可以采用构造行列式证明，Cauchy中值定理也可以采用构造行列式进行证明[2-13]。
3、二次型函数对应的矩阵
二次型函数
写成矩阵乘法的形式为
二次型函数
写成矩阵乘法的形式为:
在确定二次型的矩阵时，要注意３个方面：（1）矩阵的阶数是函数变量的个数；（2）主对角线上的元素是平方项的系数；（3）二次型中要求矩阵对称，因此第i行第j列位置上的元素是
系数的
.
如果仅从函数的角度考虑，不要求对称性，则二次型函数写矩阵乘法的形式，答案就不唯一。如
二次型要求矩阵满足对称性，则对应的矩阵就唯一。这主要是便于二次型函数求梯度及二阶偏导数矩阵。
注（1）(fx)在
上有定义，有
显然，
是偶函数，
是奇函数。因此对称区间上有定义的函数一定能表示成一个偶函数加上一个奇函数。
（2）对于任意
(不要求对称性），由于
,是对称矩阵，
是反对称矩阵。因此任意一个矩阵一定能表示成一个对称矩阵加上一个反对称矩阵。
4、函数的线性无关
在n阶线性常系数微分方程中，需要寻找基本解组，即找n个线性无关的解，这时需要利用伏朗斯基行列式的相关理论来判断解的线性相关性。设
在
上有1n-阶导数，函数
在区间上
线性无关的充要条件是其对应的伏朗斯基行列式不等于零，即
由于对任意的
行列式
所以1，
线性无关。
关于如何用线性无关的解来表示微分方程的通解，可查阅常微分方程相关文献[14-16]。
5、结语
通过学习微积分与线性代数２门课程后，会发现二者相辅相成，相互促进。可以用行列式解决微积分中的一些问题，同样也可以用微积分解决线性代数中的一些问题。虽然方法不同，但总能殊途同归，有时还能达到意想不到的效果。在教学过程中，教师应尽可能加强对微积分与线性代数间相互联系的讲解，使学生达到知识的融会贯通。
参考文献：
[1]任广千,谢聪,胡翠芳.线性代数的几何意义[M].西安:西安电子科技大学出版社,2015.
[2]王文华,陈峥立,李玮.中值定理的行列式法证明及推广[J].渭南师范学院学报,2017,32(8):26-32.
[3]刘三阳,于力,李广民.数学分析选讲[M].北京:科学出版社,2008.
[4]谭杰锋.行列式函数几何意义应用于微积分的一点注记[J].重庆工商大学学报:自然科学版,2007,24(5):435-437.
[5]苏忍锁.利用行列式构造辅助函数证明微分中值命题[J].高等数学研究,2003,6(3):26-28.
[6]朱双荣.利用行列式对柯西中值定理和拉格朗日中值定理的证明[J].高等函授学报,2009,22(5):64-65.
[7]刘文武.两个微分中值定理证明中辅助函数作法探讨[J].数学的实践与认识,2005,35(8):242-247.
[8]杨耕文.用行列式法证明微分中值定理[J].洛阳大学学报,2006,21(4):49-52
[9]王秀玲.微分中值定理的另类证明与应用[J].安庆师范学院学报:自然科学版,2010,16(4):93-95.
[10]王家军.微分中值定理的另类证明与推广[J].大学数学,2008,24(4):169-171.
[11]余丽.微分中值定理的证明及应用中的辅助函数构造[J].重庆三峡学院学报,2014,30(3):21-24.
雍龙泉.微积分中的线性代数[J].高师理科学刊,2019,39(10):55-58.
分享：
拓扑优化是一种根据给定的负载情况，约束和性能指标，优化给定区域中的材料分布的数学方法。拓扑优化的出现最初只是为了解决一般的机械设计问题。但是，随着对拓扑优化的深入研究，其已被广泛用于许多物理学科，包括固体力学、流体力学、热传导、电磁学等。此外，拓扑优化也已用于许多工程领域，例如运输、建筑设计、复合材料等。
2020-08-10
检查市场上目前可见的各种BMS拓扑的优缺点，很明显，方案之间的差异主要涉及以下问题：这是否应该是模块化BMS(即1个IC监视多个电池元件串)(图1)，或电池级BMS(即1个IC监视单个电池元件)；应该使用有线还是无线网络；并且涉及微控制器或状态机。尽管每种可用的拓扑都应该存在，但如果有解决这所有问题的硅标准可用，将加速市场采用。
2020-07-11
针对无人机编队飞行高精度相对位置感知应用，考虑通信网络时延对GNSS载波相位相对定位实时性的影响，本文分析了GNSS高精度相对定位的信息交互需求，基于图论方法优化设计了无人机编队飞行网络拓扑并设计了通信信道接入机制，对16机编队通信网络及相对位置感知进行了仿真。
2020-07-11
伴随大数据时代的到来，基于地理空间数据的拓扑分析也因其数据采集方式的改变、数据类型的多样性、数据分析目标的不同而需要采用有别于传统地理空间拓扑分析的策略．本文旨在分析大数据环境下地理空间拓扑分析的变革与特点，并结合多个实例探讨大数据环境下如何设定拓扑判定规则和分析策略，为地理空间大数据分析与应用提供一些有益的参考．
2020-07-11
关于轻量化的研究在结构工程领域已广泛开展，采用诸如拓扑优化、起筋优化、尺寸优化等一系列优化方法，可快速获取符合期望的设计方案，缩短设计周期。其中，拓扑优化的方法，是在给定的材料空间内，得到满足约束条件又使目标函数最优的材料布局方式[1]，其更多地应用于初期概念设计阶段，之后再根据材料布局，结合具体要求进行详细设计[2]。
2020-07-11
GadishDA提出了基于规则约束的方法[8]。这些方法基于拓扑关系规则和目标间语义关系，可以确定目标之间是否存在空间冲突，但具有一定的不确定性，难以准确检测，易造成漏查和误查。因此，本文将以交通网线性目标间拓扑冲突为例，通过对线目标间拓扑关系进行一致性检测，来检测已有方法造成的漏查和误查。
2020-07-11
出于环保及改善燃油耗的需求，各大车企正在快速推进汽车车体的轻量化。为实现轻量化，汽车白车身更倾向于使用高强度钢板。随着高强度钢板的应用，相应降低了板材厚度，使整个车体的刚度也随之降低。作为相关对策，使用质量最轻的材料以弥补由此降低的刚度是必不可少的。目前，可通过拓扑学最优化方法实现改良[1,2]。
2020-07-11
在5G时代来临，自动驾驶和车联网日益普及的今天，车载以太网必将得到更加广泛的推广和应用。汽车维修从业人员，有必要研究车载以太网的特性，为维修车载以太网相关故障打下良好的基础。
2020-07-11
ANSYS对结构进行了分析以及拓扑优化设计，通过拓扑优化设计可以获得初步阶段的轮廓布局，之后再重复优化步骤，可以得到较为理想的结果。本文最终优化结果体积与重量为初始体积与重量的30%左右，大大削减了复合材料的用料，同时说明了复合材料作为结构构件参与桥梁建设成为了可行的方案。
2020-07-11
社会关系是社会网的基础,编织社会的结构与功能。1社会网络被视作关系预期的动态构造,在传播中发生与发展,并且引导传播序列的进一步变化。本研究扫描当前国内大众人群的网络使用心理与行为,试图以事件传播的方式折射互联网空间的社会生态,具有推动网络安全的现实意义。
2020-07-11
人气：4546
人气：3576
人气：3354
人气：3106
人气：2962
我要评论
期刊名称：数学进展
期刊人气：3695
主管单位：中国科学协术协会
主办单位：中国数学会
出版地方：北京
专业分类：科学
国际刊号：1000-0917
国内刊号：11-2312/O1
邮发代号：2-503
创刊时间：1955年
发行周期：双月刊
期刊开本：16开
见刊时间：一年半以上
影响因子：0.553
影响因子：0.322
影响因子：0.352
影响因子：0.000
影响因子：0.000
科普杂志阅读、期刊信息查询、论文下载、文献查询、原创文章检测等多项服务。
服务热线
您的论文已提交，我们会尽快联系您，请耐心等待！
你的密码已发送到您的邮箱，请查看！
2020-03-28
552
上传者：管理员
