首页 > 论文范文 > 自然科学论文 > 数学论文 > 应用数学论文 > 基于经济学领域探究高等微积分思想的作用

基于经济学领域探究高等微积分思想的作用

2020-03-28 218 上传者：管理员

摘要：数学为科学、抽象的解决其他学科问题奠定了基础，在数学基础理论中微积分思想占有作要的位置，被广泛应用于解决各个学科的问题，在经济学领域中微积分将经济学研究的科学性及缜密性发挥到了更高的高度，有利促进行理论同实践的双重发展。文章从高等微积分思想的核心内涵着手，对其在经济学中的作用进行了研究，通过具体的实例探究微积分思想在经济学领域的具体应用，阐明微积分对于经济学领域起到的重要作用，希望能够为微积分在其他学科的应用有所裨益。

关键词：
函数模型
分析方法
经济学
高等微积分思想
加入收藏

一、高等微积分思想概述

微积分利用函数、实数以及极限等数学思想形象地阐明函数的特性以及变化规律等，作为数学分析的重要辅助工具，提供科学的演算、分析方法，主要包含积分、微分以及极限等相关知识。

（一）微分思想的核心是无限细分，即反映函数的部分变化率，用线性函数分析较小范围的函数问题。数学语言进行表述，y与x的函数关系为y=f（x），Δx、Δy是y分别在x、y轴上的变量，取函数一点A，过A点做切线，Δx在y轴方向的变量记作dy。当Δx绝对值足够小时，Δy与dy差的绝对值比Δy的绝对值要小得多，则在A点处，函数f（x）可近似用线段表示。即，原函数值近似于线性函数值。

（二）积分思想的核心是无限求和，即与微分成逆运算，已知问题的导函数求问题的原函数，包括定积分与不定积分。不定积分：利用积分运算求函数f（x）的原函数F（x），记作：∫f（x）dx=F（x）+C(C为常数)。定积分：有一定的积分区间[a，b]，函数在其上连续可积，记作，即求在区间[a，b]中函数f（x）图像所包围的面积。

二、高等微积分思想在经济学领域的应用意义

经济学问题通常较为复杂和抽象，应用微积分思想可巧妙地把问题具体化、简单化，为经济问题的解决提供准确的数据理论。微积分思想为经济决策提供科学的经济问题分析方法。当经济学领域常涉及到成本最小化、利润最大化等问题，仅仅依靠以往的经验，经济决策将缺乏科学性，而微积分思想的应用使得所要分析的问题脉络清晰，可抓住问题的关键因素，避免干扰因素的影响。例如，在进行最优化决策时，利用微积分思想中费马定理将经济效益最大值点设为极值点，该点导数为零，当经济行为偏离该点将使得经济效益下滑，因此，经济决策时遵循极值点的经济行为即可得到最大经济效益。由此可见，微积分可以实现经济资源的优化配置，将各个抽象的经济变量具体化，通过建立函数模型，对经济问题进行严谨地运算，提供准确的分析结果，从而保障经济决策的科学性、严谨性。同时，微积分思想的运用使得经济学建立与其他学科的联系，进而拓宽经济学研究范围与研究角度。

三、微积分思想在经济学领域的相关应用

本文将通过具体的实例探究微积分思想在经济学领域的具体应用，阐明微积分对于经济学领域起到的重要作用。问题一提出：某企业生产成本C与产量Q之间的函数关系C（Q）=3Q+150，收入R与产量Q的函数关系R（Q）=264Q－Q2。求企业生产多少数量产品可使得利润L（Q）达到最大?利用微分思想解答此问题的思路是，这是最优化问题，首先建立利润与收入、成本之间的函数关系，L（Q）=R（Q）－C（Q）=261Q－Q2－150，然后函数关系关于利润求导，求极值点即导函数为零，L'（Q）=0，求得的产量值即问题所求。问题二提出：某企业边际收入R'（x）=8－x，固定成本为1.5万元，边际成本C'（x）=4，试求企业产量与利润多少时，获利最大？利用积分思想解答此问题的思路是首先，总利润L（x）=R（x）－C（x），则边际利润L'（x）=R'（x）－C'（x）=4－x，令其为零，求解出驻点，驻点即处企业获利最大时的产量值。同时企业的总收入函数，总成本函数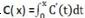，根据驻点值即可求出最大利润。

综上所述，经济学科与微积分思想的有效结合，能够使得经济学问题更为清晰、可控。通过函数分析与变量分析，以新的视角分析经济学问题，排除干扰因素对问题的影响，把握问题的关键，为问题分析提高更为准确的结果，提高经济决策的科学性与严谨性。本文基于阐述高等微积分思想的核心内涵，探讨微积分思想对于经济学的重要意义，并结合实例分析微积分思想在经济学领域的相关应用，可见，微积分思想解决经济问题既普遍又重要，建议经济学研究不断加强微积分思想与经济学科的融合与发展。

参考文献:

[1]李培.试论高等数学中微积分的经济应用分析[J].当代教育实践与教学研究,2018(11):176-177.

[2]吕卫平,吴善和,马奕.转型发展背景下经管类专业微积分课程教学改革研究[J].黑河学院学报,2018,9(07):134-135.

[3]谢锡麟.基于数理知识体系自身与传播研究的微积分教学[J].复旦学报(自然科学版),2018,57(02):250-270.

郑贺.高等微积分思想及其在经济学领域中的应用探讨[J].环渤海经济瞭望,2019(8):162-162.