理想的轴心受压构件不存在初始偏心。对于实际工程中的钢筋混凝土柱，受到材料不均匀、施工误差、荷载偏差等多种因素的影响，不可避免地存在一定的初始偏心，轴向压力作用在构件的各个截面产生了附加弯矩。钢筋混凝土短柱的二阶效应较小，此附加弯矩对其受力性能影响不大；中长柱和细长柱的二阶效应较大，附加弯矩作用下构件将发生明显的侧向挠度，在轴向压力和弯矩共同作用下构件发生破坏。对于配置螺旋箍筋的混凝土柱，在轴心压力作用下，由于螺旋形布置的箍筋对核心区混凝土的约束套箍作用，可以显著提高其承载能力和延性。对于螺旋箍筋约束混凝土力学性能，国内外开展大量的理论、试验研究和数值模拟，早在1929年，Illinois大学开展了螺旋箍筋柱的力学性能试验[1]，李青宁、张兴虎开展了螺旋箍筋柱抗震性能的试验研究[2,3]，冯永伟开展了螺旋箍筋柱抗剪性能的研究[4]，丁慧、张松开展了螺旋箍筋柱的延性分析[5]及受理机理的研究[6]，Chen,Y、Sun,Lin-Zhu研究了多层螺旋箍筋柱的受压性能[7,8]，Kim,J.K研究了尺寸对素混凝土柱和螺旋箍筋柱体抗压强度的影响[9]，Liang,Ching-Yu研究了多层螺旋箍筋方形混凝土柱的轴向受压性能[10]，等。然而，已有的研究绝大多数针对长细比较小的短柱，对长细比较大的螺旋箍筋柱的研究较少。我国GB50010-2010规范中对于配置螺旋箍筋的混凝土柱（λ≤12）的轴心受压承载力计算公式中，未考虑长细比和稳定性对其力学性能的影响。关于长细比对螺旋箍筋柱的力学性能影响的研究，目前国内外未见公开的报道。

为了定量分析长细比对配置螺旋箍筋的混凝土柱轴心受压性能的影响，本文基于ANSYS有限元分析平台建立了螺旋箍筋柱的精细化有限元分析模型，利用既有的试验结果进行了模型验证。在此基础上，开展了有一定初始偏心的不同直径和长细比的螺旋箍筋柱轴心受压破坏过程的数值模拟，分析了长细比对螺旋箍筋柱轴心受压性能的影响规律，并提出了螺旋箍筋柱轴心受压承载力计算公式中稳定系数的取值建议。

1、国内外规范承载力计算的比较

目前，国内外主流的混凝土结构设计规范中，关于是否考虑及如何考虑长细比对轴心受压构件稳定性及承载能力的影响的规定差异较大。现选择其中几种有代表性的规范进行对比，如表1所示。

表1中国内外有关规范关于钢筋混凝土轴心受压构件的计算公式的对比分析表明，除了BS8110:1997规范未区分其与普通箍筋柱的差别外，GB50010-2010、JSCE-2007规范通过等效间接钢筋的方式考虑螺旋钢筋约束混凝土的贡献，ACI318-2014规范则在普通箍筋柱的承载力计算值的基础上乘以0.85/0.80的增大系数。配置普通箍筋的混凝土柱的正截面受压承载力计算中，除GB50010-2010规范之外，国外混凝土结构设

表1混凝土结构设计规范中承载力计算公式的比较

注：表中各参数的物理意义详见对应的技术标准。

计规范中均未单独考虑长细比对构件轴心受压承载力的影响；除GB50936-2014规范规定钢管混凝土柱外，其他标准均未明确考虑长细比对螺旋箍筋的混凝土柱轴心受压承载力的影响。

实际工程中，绝对的轴心受压是不存在的，因此，钢筋混凝土构件的轴心受压承载力应考虑偶然偏心的影响。由于轴力N偶然偏心引起的弯矩及其二阶效应的影响，实际工程中钢筋混凝土构件的轴心受压承载力将低于理想的轴心受压构件的承载力，且随着构件长细比的增大，二阶效应的影响将越来越显著。GB50010-2010规范中普通箍筋柱正截面承载力计算公式中考虑长细比的影响概念清楚，物理意义明确；但是螺旋箍筋柱的承载力计算公式中未考虑长细比对承载力的影响，二者存在不一致性。尽管普通箍筋柱和螺旋箍筋柱核心区混凝土的受力状态存在一定的差异，螺旋箍筋柱的核心区混凝土存在显著的横向约束作用，但是对于GB50936-2014规范中横向约束更强的钢管混凝土柱，也考虑了长细比对承载力的影响。此外，当螺旋箍筋柱的长细比λ=l0/d=12时，按照普通箍筋柱的稳定系数计算公式得出的稳定系数系数φ=0.92。考虑到螺旋箍筋柱达到其承载能力极限状态时，混凝土保护层往往均已开裂和剥落，因此其核心区的长细比λcor=l0/dcor将更大，对应的稳定系数更小，忽略长细比和稳定性对轴心受压承载力的影响是不合适的。因此，本文建议GB50010-2010规范修订时，螺旋箍筋柱正截面受压承载力计算公式中增加稳定系数以考虑长细比对其承载力的影响，主要修订建议如下：

（1）螺旋箍筋柱轴心受压承载力计算公式中增加稳定系数以考虑长细比对承载力的影响，确保受压构件计算理念和表达形式的一致性；

（2）螺旋箍筋柱的长细比根据核心区的横截面计算确定，并据此确定螺旋箍筋柱的稳定系数与λcor的函数关系。

参考GB50010-2010规范中普通箍筋柱轴心受压承载力计算公式，建议考虑初始偏心影响的螺旋箍筋柱轴心受压承载力计算公式修正为：

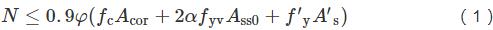
式中：φ为与螺旋箍筋柱的长细比λcor有关的稳定系数，即φ=φ(λcor)；其他符号的物理意义与GB50010-2010规范一致。

2、承载性能的有限元模拟

为了分析长细比对配置螺旋箍筋的混凝土柱轴心受压性能的影响，基于ANSYS通用有限元分析平台，建立了配置螺旋箍筋的混凝土柱的非线性有限元分析模型，并利用既有的试验结果进行了模型的验证。

2.1混凝土的本构模型

在配有纵筋和螺旋箍筋的混凝土柱中，轴向压力作用下核心混凝土和螺旋箍筋存在着相互作用，需要考虑螺旋箍筋对核心区混凝土的约束作用。本文借鉴了文献[16]中钢管混凝土常用的考虑横向约束效应的核心混凝土本构模型，核心混凝土的应力-应变（σ-ε）模型如图1(a)所示，其表达式为：

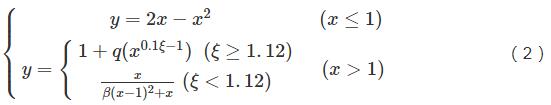
式中x=ε/ε0，y=σ/σ0，ξ为约束效应系数。其余参数意义及其表达式可参见文献[16]。

2.2钢筋应力-应变关系

钢筋采用考虑硬化效应的弹塑性本构模型，选用经典的vonMises屈服准则。普通低碳钢筋应力-应变关系如图1(b)所示，其表达式[17]如下：

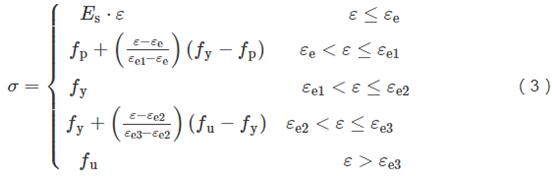
式中：fp、fy、fu分别为钢材的弹性极限、屈服强度、极限抗拉强度。取εe=0.8fy/Es，εe1=1.5εe，εe2=10εe1，εe3=100εe1。

高强钢材选用双线性强化模型，强化段的模量为0.01Es，Es为钢材弹性模量，如图1(c)所示。

图1核心区约束混凝土和不同钢材的σ­ε关系

2.3有限元模型建立

2.3.1单元类型的选取和网格的划分

螺旋箍筋柱采用钢筋-混凝土分离式建模，如图2。为了控制计算规模，两端铰支螺旋箍筋柱只取1/2进行有限元建模，模型的中面上施加对称约束。螺旋箍筋柱的保护层混凝土和核心区混凝土均采用SOLID65实体单元模拟，螺旋箍筋及受压纵筋均采用LINK180单元模拟。混凝土实体采用六面体单元进行映射网格划分，横截面上标准网格大小取30mm。螺旋箍筋采用APDL语言实现了空间螺旋线的建模，控制螺旋箍筋柱轴向单元的网格尺寸为30mm左右，保证螺旋箍筋单元尺寸小于核心区混凝土单元尺寸。不考虑箍筋与混凝土之间的滑移，纵筋与混凝土单元通过merge节点实现耦合，螺旋箍筋单元节点通过约束方程Ceintf方式与核心区混凝土建立约束关系。

图2螺旋箍筋柱的空间有限元模型

2.3.2边界条件和加载方式

螺旋箍筋柱有限元模型顶面所有节点与钢垫板底面进行共节点耦合，钢垫板顶面采用MPC方法通过一点与顶面所有节点建立刚性梁进行约束。最终通过在刚性梁单元上施加位移或内力的方式进行加载。模型的底面为两端铰支螺旋箍筋柱的对称面，在模型的底面施加对称约束。为得到曲线的下降段，采用位移控制加载，并采用增量迭代法进行非线性方程组的求解。纵筋受压屈服以后，螺旋箍筋外侧的保护层混凝土开始开裂和剥落，带来了计算收敛性问题。为了保证收敛，提高计算效率，当受压纵筋临近屈服时，采用生死单元的方法杀死保护层混凝土单元，只保留螺旋箍筋、纵筋以及核心区混凝土部分的有限元模型继续后续的计算。

2.4模型的试验验证

为了验证本文建立的螺旋箍筋柱的空间有限元模型及模拟方法的可行性，对文献[1]中数据完整的4组12根螺旋箍筋柱试件的轴压加载过程进行了ANSYS模拟。

文献[1]中螺旋箍筋柱试件设计为直径254mm，高度1016mm，长细比λ=4。螺旋箍筋分别采用低碳软钢和高强钢材两种，具体材料及结构参数参见文献[1]。上述各组试件的极限承载力的试验结果、数值模拟结果及GB50010-2010规范公式计算结果的对比如表2所示。其中规范公式计算时材料强度指标采用试验实测值，不考虑可靠度调整系数。由表2可知，采用本文ANSYS数值模拟得出的各组试件的极限承载力与文献[1]中四组试件的试验结果吻合较好，最大误差仅为2.32%，可见GB50010-2010规范公式的计算结果与文献[1]试验结果、ANSYS数值模拟结果吻合较好。

采用螺旋箍筋柱顶面中心点和底面中心点之间距离的变化量与箍筋柱初始长度的比值表示其变形，将本文数值模拟得出的螺旋箍筋柱荷载-变形(P-ε)曲线与文献[1]试验实测结果进行了对比，如图3所示，本文数值模拟结

表2ANSYS模拟结果与试验结果的比较

果总体上与文献[1]试验结果吻合较好。因此，采用本文的有限元建模和数值模拟方法模拟螺旋箍筋柱的力学行为是可行的。

图3有限元模拟结果与试验结果[1]的比较

3、长细比对承载力的影响分析

利用本文的有限元建模和数值模拟方法，建立了三组不同直径、不同长细比的螺旋箍筋柱的非线性有限元分析模型，进行了轴向压力作用下螺旋箍筋柱破坏过程的数值模拟，以定量分析长细比对配置螺旋箍筋的混凝土柱轴心受压承载性能的影响规律。

3.1计算工况

螺旋箍筋柱的混凝土强度等级为C40，柱中纵筋及螺旋箍筋均采用HRB400级钢筋，箍筋的螺距s相同，纵筋沿核心区外围圆周边均匀布置。三组模型具体参数如下：（1）核心区直径为dcor=400mm，纵筋为818，螺旋箍筋为10@60；（2）核心区直径dcor=500mm，纵筋为820，螺旋箍筋为12@60；（3）核心区直径dcor=600mm，纵筋为822，螺旋箍筋为14@60。每一组14个构件，相应的长细比l0/dcor依次从2逐步增大至15。考虑到初始偏心对螺旋箍筋中长柱和长柱的轴压力学性能影响较大，参考文献[16]的模拟方法，本文的螺旋箍筋柱有限元分析时轴向荷载考虑了e0=l0/1000的初始偏心。

3.2长细比对螺旋箍筋柱荷载—变形的影响

采用本文的有限元建模和数值模拟方法，得出了每一组内相同直径不同λcor的螺旋箍筋柱轴心受力性能变化规律。以第3组dcor=600mm的螺旋箍筋柱为例，不同典型λcor的螺旋箍筋柱的荷载-变形（P-ε）曲线如图4所示。从图4可以看出，当轴压荷载水平较低（如极限荷载Pu的60%~70%）时，不同λcor的螺旋箍筋柱的P-Δ/l曲线几乎重合，此时钢筋混凝土材料尚处于弹性阶段；随着轴压荷载的增大，随着混凝土塑性变形的发展和受压纵筋及螺旋箍筋的应力相继达到屈服强度，初始偏心引起的附加弯矩的影响将越来越大，随着构件长细比的增大，材料非线性和几何非线性的影响也越来越大，螺旋箍筋柱的屈服平台越来越短，构件由λcor较小时的延性破坏逐渐转变为λcor较大时的脆性破坏。螺旋箍筋柱轴心受压极限荷载和λcor密切相关，λcor越大构件的极限承载力越低，破坏时极限应变也越小，屈服平台越短，曲线下降段也越陡，构件的塑性越差。

图4不同λcor螺旋箍筋柱的荷载-变形P-ε曲线

当构件的长细比较大时，轴力的初始偏心作用下使构件产生侧向挠曲，二阶效应大大增大了附加弯矩及构件侧向挠度，螺旋箍筋中长柱和长柱最终在轴力和弯矩共同作用下发生破坏。图5（a）、（b）和（c）分别给出了dcor=600mm，λcor=12的螺旋箍筋柱混凝土轴向应力、塑性应变和开裂应变分布图。由图5可以看出，底部在轴力和最大弯矩共同作用下，螺旋箍筋柱破坏时，在螺旋箍筋柱底部沿着初始偏心一侧轴向压应力达到最大，该位置出现较大的塑性变形，远离初始偏心一侧受拉，受拉区出现明显的开裂应变。

图6为不同长细比的螺旋箍筋柱具有初始偏心的轴力作用下的荷载P—侧向挠度f曲线。由图6可见，开始加载时螺旋箍筋柱的侧向挠度与荷载基本成正比；当荷载达到极限荷载Pu的60%~70%后，侧向挠度随着荷载增加的增长速度明显加快；当荷载达到构件的极限承载力之后，侧向挠度急剧增加，构件进入了软化阶段，承载力缓慢减小。长细比越大，相同的荷载作用下侧向挠度越大，破坏时构件的横向挠曲变形越大，二阶效应对其轴心受压承载性能的影响越显著。

图5柱临近破坏时混凝土应力应变云图

图6不同长细比螺旋箍筋柱的P-f曲线

表3螺旋箍筋柱轴心受压的有限元模拟结果

3.3螺旋箍筋柱的稳定系数

本文开展了核心直径分别为400/500/600mm，不同核心区长细比λcor的螺旋箍筋柱的轴心受压行为的数值模拟，计算结果详见表3。由表3可知，随着λcor的增大，螺旋箍筋柱的轴压极限承载力有不同程度的降低。当λcor≤5时，其极限承载力较λcor=2对应值下降幅度较小，低于3.7%；随着λcor的继续增大，螺旋箍筋柱轴心受压极限承载力降低幅度将持续增大，λcor达到15时其极限承载力较λcor=2时对应值下降了25%左右，可见对中长柱和长柱，λcor对其轴心受压极限承载力影响显著，不能忽略不计。

图7为根据有限元分析结果得出三组不同核心直径螺旋箍筋柱计算稳定系数随着长细比的变化曲线。由图7可见，随着核心区长细比λcor的增大，稳定系数逐渐降低，且λcor越大，降低的幅度也越来越大。当λcor保持不变，核心直径dcor较小时，螺旋箍筋柱的稳定系数略高于直径较大时的相应值。当dcor达到500~600mm时，稳定系数计算结果趋于稳定，差距在0.2%以内。

采用Origin软件对图7中有限元模拟得出的稳定系数和长细比进行数据的非线性拟合，得出考虑初始偏心影响的螺旋箍筋柱稳定系数φ的计算公式为：

φ=1.0169−11000[0.654(l0dcor)2+7.660l0dcor]（4）

式中l0/dcor为核心区长细比，2≤l0/dcor≤15。

图7不同长细比的螺旋箍筋柱的稳定系数

ANSYS有限元计算得出不同核心区长细比λcor的螺旋箍筋柱稳定系数与式（4）计算结果的比较如表4所示。由表4可见，式（4）计算得出的稳定系数与有限元计算结果的误差为-0.457%~0.631%，二者吻合较好。因此，本文建议，对于核心区长细比λcor为2~15范围内的螺旋箍筋柱，其轴心受压承载力计算公式（1）中的稳定系数φ可按式（4）计算确定，也可查表4确定，当核心区长细比λcor不为整数时，稳定系数可采用线性插值确定。

表4螺旋箍筋柱轴心受压稳定系数φ

长细比λcor

有限元计算φfea

式(4)计算φcal｜φcal-φfea｜/φfea

4、结论

1）通过国内外主流混凝土结构设计规范有关轴心受压构件承载力计算公式的对比分析，提出了考虑初始偏心和核心区长细比（λcor=l0/dcor）影响的螺旋箍筋柱轴心受压承载力计算公式的修订建议。

2）通过精细化非线性有限元分析，研究了不同长细比和不同核心直径的螺旋箍筋柱轴心受压性能的变化规律。结果表明，其极限承载力与构件核心区长细比λcor密切相关，λcor越大构件极限承载力越低，临近破坏时极限压应变越小，荷载-位移曲线下降段也越陡。

3）核心区长细比λcor≤5时，螺旋箍筋柱的极限承载力随着长细比增加而降低的幅度较小，低于3.7%；随着λcor的继续增大螺旋箍筋柱的极限承载力降低幅度逐渐增大，λcor达到15时，其极限承载力较λcor=2.0对应值下降了25%左右。可见，螺旋箍筋柱λcor对其承载力的影响明显，对于长细比较大的中长柱和长柱，λcor的影响不可忽略。

4）有限元分析结果表明，当螺旋箍筋柱的核心直径达到500~600mm时，其稳定系数趋于稳定。基于有限元分析结果，提出了考虑初始偏心影响的螺旋箍筋柱轴心受压的稳定系数φ的回归公式和取值建议。

参考文献：

[2]李青宁,郑先超,颜志勇,等.高强螺旋箍筋约束混凝土柱连接抗震性能试验研究与理论分析[J].建筑结构学报,2013,34(8):90-99.

[3]张兴虎,郑晓龙,潘树宾,等.高强螺旋箍筋约束混凝土柱抗震性能试验[J].建筑科学与工程学报,2013,30(2):21-27.

[4]冯永伟.高强混凝土高强连续复合螺旋箍筋柱抗剪性能的研究[D].西安:西安建筑科技大学,2004.

[5]丁慧,陈兰响,樊成.双层高强螺旋箍筋约束混凝土轴压短柱强度和延性的研究[J].水利与建筑工程学报,2015,13(3):60-65.

[6]张松.配置圆形复合螺旋箍筋的钢筋混凝土方柱力学性能研究[D].哈尔滨:哈尔滨工业大学,2016.

[11]混凝土结构设计规范:GB50010-2010[S].北京:中国建筑工业出版社,2011.

[15]钢管混凝土结构技术规范:GB50936-2014[S].北京:中国建筑工业出版社,2014.

[16]韩林海.钢管混凝土结构:理论与实践[M].第2版.北京:科学出版社,2007.

[17]何青龙.钢管混凝土柱-钢筋混凝土梁节点力学性能的有限元模拟[D].成都:西南交通大学,2016.

刘晓春,谢绍辉,余志武,杨义益,祁敏.长细比对螺旋箍筋柱轴心受压承载力的影响[J/OL].建筑结构学报:1-9[2020-06-28].

基金:国家自然科学基金项目(U1434204);;国家重点研发计划项目(2017YFB1201204);;湖南省自然科学基金项目(2019JJ40383).