首页 >
论文范文 >
自然科学论文 >
化学论文 >
理论化学论文 >
基于熵的纠缠演化探讨纠缠腔场和纠缠Ξ-型三能级原子的关系
摘要：文章利用一对处于纠缠态的Ξ-型三能级原子与一对处于纠缠态的单模腔场,初始时刻原子与腔场之间互不纠缠,使其中一个原子与一个腔场发生相互作用,即纠缠交换,合适选择相互作用时间就可实现原子与腔场之间产生纠缠,并研究了系统原子熵的演化特性,运用量子熵理论,讨论了原子-腔场的耦合常数对原子熵的影响,结果表明:原子与光场跃迁耦合常数对系统熵的最大纠缠度有影响.当原子与光场两种跃迁耦合常数之比k值增大时,最大纠缠度在减小;当k增大到某一程度时,系统熵随时间周期性变化,并出现双峰现象.
加入收藏
1、引言
量子纠缠是量子信息和量子计算的核心,而且在量子通信领域中有着广泛而重要的应用[1].例如:量子隐形传送[2]、量子密钥[3]、量子密集编码[4]等.为了进行纠缠态的远距传送,往往需要事先让相距遥远的两地共同拥有最大量子纠缠态,但是由于受外界环境噪声的影响,就会不可避免地导致不同程度的纠缠品质下降,在此背景下就提出了纠缠交换[5],其目的是通过某些物理过程,使从未发生直接相互作用的量子系统之间产生量子纠缠.这对于建立远程非局域关联是非常有用的.
原子与光场相互作用时可表现出一些非经典效应,如:原子周期的崩塌-回复、光场的压缩特性、光场的聚束与反聚束等,这些都反映了场和原子的量子特性,但是这些效应还不能完全说明其相互作用的动力学的量子特征,熵是一个描述系统偏离纯态程度的物理量,在量子信息领域有着非常重要的应用,根据Phoenix和Knight[6,7]提出的量子约化熵理论,光场与原子相互作用时,可以通过熵随时间的演化来反映原子与场之间的关联程度,熵值越大,关联程度越大,在熵值的最大区域,若想最大限度地获得光场所包含的信息可以通过对原子的测量来实现,所以,研究反映原子与光场关联效应的场(原子)熵有很重要的实际意义.近几年,人们研究两能级原子与光场、三能级原子与光场相互作用系统熵的演化特性的较多[8,9,10,11,12],但研究原子与光场经过纠缠交换之后,两者之间产生纠缠的系统熵的演化甚少提及.本文基于纠缠的两个Ξ-型三能级原子与两个纠缠的单模腔场,初始时原子与腔场互不纠缠,让其中一个原子和一个腔场发生共振相互作用,得到了两原子与两腔场纠缠交换后的系统的熵,并利用量子熵理论,讨论了原子与腔场跃迁的耦合常数对系统熵的影响.
图1与单模腔场相互作用的三能级原子示意图
2、理论及模型
考虑一个三能级原子与一个单模腔场通过双光子J-C模型发生相互作用,在相互作用绘景中,哈密顿量可表示为
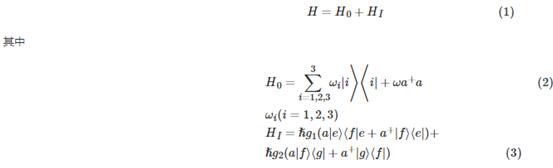
g1、g2分别表示|e〉↔|f〉、|f〉↔|g〉之间发生跃迁的耦合常数.下图1给出了原子能级示意图.其中,ωi(i=e,f,g)分别是对应于原子能级|e〉、|f〉、|g〉的频率,原子与腔场整个系统的演化可用下式表示
图1与单模腔场相互作用的三能级原子示意图
根据薛定谔方程,结合式子(3)、(4),我们可以得到下面三个耦合的微分方程
假定原子与腔场的初始态(初始时间t=0)是
Cn(0)表示任意初始场态的振幅,以及Ca(0)(a=e,f,g)是初始原子态(归一化)|χ〉=Ce|e〉+Cf|f〉+Cg|g〉的振幅,根据这些初始条件,解薛定谔方程,可得到以下系数
其中
,是拉比频率,分别在式子(8)、(9)中做代换n→n-1、n→n-2,就可得到Cf,n(t)和Cg,n(t).
假定两个原子(1,2)和两个腔场(3,4)最初分别处于态|φ〉12=α1|g〉1|e〉2+β1|e〉1|g〉2和|φ〉34=α2|2〉3|0〉4+β2|0〉3|2〉4,如图2所示,最初,两个原子之间存在纠缠,两个腔场之间存在纠缠,但是原子1,2与腔场3,4之间互不纠缠,其中|0〉表示真空态,|2〉表示双光子态,接着原子2与腔场3发生相互作用,系统态随时间的演化为
其中,C(u,v)x,y表示式子(15)中的系数,考虑到系统最初态处在(u,v),x,u代表原子所处态,y,v代表腔场所处态.
图2纠缠交换方案示意图|φ〉12表示两原子(1,2)间的纠缠;|φ〉34表示两光场(3,4)间的纠缠
3、纠缠交换
通过纠缠交换,整个系统的密度矩阵为
ρ=|φ⟩12341234⟨φ| (11)
最初原子系统与光场系统都处于纯态,并且彼此之间没有相互作用,因此,整个原子-光场系统的熵为零并保持恒定,根据Araki-lieb不等式[13],原子系统、光场系统的熵满足
|Sa−Sf|≤S≤|Sa+Sf| (12)
对于任何t>0的时刻,都有S=0,因而任意时刻光场系统的熵都等于原子系统的熵,对光场(3,4)求迹可得出原子约化密度矩阵
4、数值计算与讨论
将λ的值(15)式代入(14)式可以求出系统原子熵,图3给出了原子1,2与光场3,4最初分别处于最大纠缠态,即α1=β1=α2=β2=1/2√时,原子与光场两种跃迁耦合常数之比k=g2/g1不同时,系统熵随时间的演化情况,图3(a)～(e)显示了原子-腔场的耦合常数对系统熵的影响.由图像可知,当k=1,熵随时间出现不规则的震荡(如图a),随着k值的增大,系统的最大纠缠度在减小,熵的图像逐渐呈现出类似的双峰现象,即纠缠度先增大后减小,减小到某个值后继续增大,然后再减小到最小,并且双峰的周期明显在变短,两个峰的大小也不对称,但当k=20时,两原子的纠缠出现周期性变化,双峰现象非常明显且两峰大小对称,即纠缠度先增大后减小,减小到某个值后继续增大,然后再减小直到完全分离.可见,原子与光场跃迁耦合常数对系统熵有一定的影响.
图3原子-腔场的耦合系数对原子熵的影响.
5、结论
本文基于两个Ξ-型纠缠的三能级原子与两个纠缠的腔场双光子共振相互作用,得到了两个纠缠原子与两个腔场纠缠交换后的系统的原子熵,并利用量子熵理论,讨论了原子与光场跃迁耦合常数对系统熵的影响,结果表明:系统熵的最大纠缠度随原子与光场两种跃迁耦合常数之比k的增大而减小,当k增大到某一程度时,系统熵随时间周期性变化,并出现双峰现象.
参考文献:
[8]刘翔,方卯发.光场与级联型三能级原子相互作用时的熵特性和薛定谔猫态[J].物理学报,2000,49:1707]
[9]卢道明.级联三能级原子与相干光场相互作用场熵的演化[J].原子与分子物理学报,2006,23:912]
[10]刘素梅.非旋波近似下光场与级联型三能级原子相互作用系统场熵的演化特性[J].量子电子学报,2003,20:725]
[11]张金芳,谭磊,刘利伟,等.运动级联型三能级原子双光子过程的熵的演化[J].物理学报,2008,57:2205]
[12]李永平,刘永亮,贺金玉.失谐量对“单模真空场-Ξ型三能级原子”相互作用系统场熵压缩特性的影响[J].量子电子学报,2003,20:715]
张蕾,郝丹辉,强稳朝.纠缠Ξ-型三能级原子与纠缠腔场相互作用熵的纠缠演化[J].原子与分子物理学报,2020,37(05):734-738.
基金:陕西省教育厅科研项目(18JK025).
分享：
水质化学分析要求专业人员应用相应的化学试剂、合理的检测方法以及先进的检测设备等对水体的各项指标进行有效检测。在实际开展水质化学分析工作时，检验人员需要依据不同地区具体的水质情况，采取对应主成分分析法、模糊综合监测法等分析方法，严格依据样品采集、储存以及运输等不同环节的要求进行检验。
2023-09-01
有机膦-金配合物作为催化剂在有机合成反应中的应用一直是催化研究领域的热点之一,许多金配合物被证实能有效地催化活化炔烃、烯烃,甚至芳香化合物。然而大部分有机膦-金配合物具有催化活性的中间体稳定性不好,导致其催化活性及应用受到诸多限制,因此合成新型的有机膦-Au配合物并研究其结构与性质具有重要的意义。
2020-07-16
通信设备给生活带来便利的同时,也带来了日益严重的电磁干扰[1,2,3,4,5].长期生活在电磁辐射环境中,会给人的身体和心理带来不良影响,如人体免疫力降低.随着电子设备小型化,元器件间的电磁波相互干扰,进而缩短设备的使用寿命.手机辐射的电磁波会对精密仪器产生一定的干扰,影响仪器的正常工作.在雷达探测中,电磁干扰会导致军事打击的准确性降低[6,7].
2020-07-14
劳氏紫是一种含有N和S的有机试剂，和Hg(II)之间有较强的结合力。本研究采用化学键合方法，将劳氏紫联接到磁性纳米材料表面，制备一种劳氏紫修饰的功能化核壳型磁性纳米材料，对其进行表征，测试其磁响应性能，并研究对废水中重金属Hg(II)的吸附性能，以期对含Hg(II)废水的吸附处理具有借鉴作用。
2020-07-09![探讨{[Zn(L)(CH3COO)]•(H2O)}n(1)的结构表征与合成方法](https://91xueshu.oss-cn-qingdao.aliyuncs.com/uploads/2019/11/5ddf193d18cac_thumb.jpg)
本文选择了一个含苯甲酸和苯并咪唑基团的双功能配体4-(2-苯并咪唑基)苯甲酸(L)(Scheme1)。该配体中既有芳香羧基又有咪唑环，这两个基团都有很强的配位能力，协同效应下应该会制备出具有新颖结构和性能的配位聚合物。最终，在水热条件下，我们合成了L与Zn(II)的配位聚合物{[Zn(L)(CH3COO)]∙(H2O)}n(1)。X-射线单晶衍射实验发现该配位聚合物为2D结构。
2020-06-29
高校物理化学实验是一门重要的化学基础学科，在巩固加深物理化学理论课程中概念和理论的理解方面有着重要作用。中国海洋大学是一所具有海洋特色的综合性学校，涉海学科一直是我校特色优势化学科，如何结合当代蓝色经济发展的需求，将海洋特色和各专业特色融入到目前实验教学内容当中，丰富实验内容，激发学生学习兴趣，一直是我们实验教学队伍的研究内容。
2020-06-29
超级电容器作为当代应用最为广泛的绿色储能装置，在各市场领域发展前景广阔[1,2]。但因其能量密度不高、使用寿命短等缺陷而无法满足人们对超级电容器的更高性能需求，所以仍需对其性能进行改善。超级电容器性能的高低与电极材料的性能直接相关，而影响电极材料的电化学性能的主要因素有溶液pH、反应物的用量（比例）及反应温度等。
2020-06-29
本文首先通过水热法合成球状TiO2纳米颗粒，利用NaBH4在高温条件下将其还原成黑色TiO2，减小带隙增强对可见光的吸收。然后，将黑色TiO2颗粒在高温条件下与MoS2粉末相结合构建黑色水热法TiO2/MoS2异质结，有效抑制了光生空穴对的重合。同时，利用扫描电子显微镜（SEM）进行形貌结构分析。
2020-06-29
甲醇重整燃烧电池（以下简称“甲醇电池”）为了结构紧凑、控制便利，重整和启燃时均以甲醇水溶液为原料；冷启动时，热量主要由甲醇水溶液气化燃烧供给。因启动温度低、甲醇水溶液气化不足、氧化燃烧催化剂不耐湿、尾气空速大等因素，甲醇难充分燃烧，尾气中常存在一定的甲醇、甲醛等。
2020-06-29
在本文中,我们制备出具有中孔结构的TS-1分子筛,以它作为基底将金属Ga3+离子修饰于分子筛TS-1的表面,得到Ga3+离子改性的中孔分子筛材料。在室温紫外光辐照条件下,考察中孔结构对乙烷C—H键的活化以及对目标产物转化的影响。结果显示,中孔Ga3+-TS-1分子筛显示出极高的光诱导活化乙烷C—H键生成丁烷的能力。
2020-06-29
人气：5061
人气：4841
人气：3884
人气：3675
人气：2600
我要评论
期刊名称：化学学报
期刊人气：5665
主管单位：中国科学院
主办单位：中国科学院上海有机化学研究所,中国化学会
出版地方：上海
专业分类：化学
国际刊号：0567-7351
国内刊号：31-1320/O6
邮发代号：4-209
创刊时间：1933年
发行周期：月刊
期刊开本：大16开
见刊时间：一年半以上
影响因子：2.741
影响因子：1.160
影响因子：1.215
影响因子：0.770
影响因子：0.374
科普杂志阅读、期刊信息查询、论文下载、文献查询、原创文章检测等多项服务。
服务热线
您的论文已提交，我们会尽快联系您，请耐心等待！
你的密码已发送到您的邮箱，请查看！
2020-05-29
196
上传者：管理员
