首页 > 论文范文 > 自然科学论文 > 数学论文 > 数学分析论文 > 试论考研数学中微分中值定理的应用

试论考研数学中微分中值定理的应用

2020-06-30 606 上传者：管理员

摘要：微分中值定理是微积分学中的重要基本定理,也是考研数学中的重要考点,学生普遍认为微分中值定理的应用是学习的难点．本文以考研真题为例,来讨论微分中值定理的应用。

关键词：
不等式
原函数法
微分
微分中值定理
数学分析
加入收藏

微分中值定理是微分学理论的重要组成部分，起着建立函数与其导数之间的桥梁作用，也是研究函数变化形态的纽带，因此在微分学中的地位十分重要。同时也是考研数学中的重要考点，学生普遍认为是学习的难点。本文对考研真题进行剖析，总结中值定理的应用，以便学生能更好地掌握这一知识点。

例1(2011年数一、二)证明:对任意正整数n，都有成立。

证明:根据拉格朗日定理，存在ξ∈(n,n+1)，使得

若所证不等式中出现函数值差的形式，可考虑用根据拉格朗日定理。本题中，令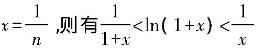。该结论是一个常用的结论，希望考生熟悉掌握。

例2(2007年数一、二、三)设函数f(x),g(x)在[a,b]上连续，在(a,b)内具有二阶导数且存在相等的最大值，f(a)=g(a),f(b)=g(b)，证明:存在ξ∈(a,b)，使得f″(ξ)=g″(ξ)。

分析:若令F(x)=f(x)-g(x)，本题需要证明存在ξ∈(a,b)，使F″(ξ)=0，又F(a)=F(b)=0，若能证明存在η∈(a,b)，使F(η)=0，对F(x)反复用罗尔定理可证明本题。

证明:令F(x)=f(x)-g(x)，则F(a)=F(b)=0。设f(x),g(x)在(a,b)内的最大值为M。且分别在α∈(a,b)，β∈(a,b)取到，即f(α)=M,g(β)=M。⑴若α=β，取η=α，则F(η)=0;⑵若α≠β，则F(α)=f(α)-g(α)=M-g(α)0,F(β)=f(β)-g(β)=f(β)-M#0。此时，由连续函数介值定理知在α与β之间至少存在点η，使F(η)=0。综上所述，存在η∈(a,b)，使F(η)=0，由罗尔定理知存在ξ1∈(a，η)，ξ2∈(η，b)，使得F'(ξ1)=0,F'(ξ2)=0，再由罗尔定理得，存在ξ∈(ξ1，ξ2)(a,b)，使得F″(ξ)=0，即f″(ξ)=g″(ξ)。

一般地，证明存在ξ∈(a,b)，使f(n)(ξ)=0的命题的有效方法是证明f(n-1)(x)在(c,d)[a,b]上满足罗尔定理，对f(n-1)(x)应用罗尔定理即可证得命题。

例3(2017年数一、二)设函数f(x)在区间[0,1]上具有2阶导数，且。证明:

(1)方程f(x)=0在区间(0,1)内至少存在一个实根;

(2)方程f(x)f″(x)+[f'(x)]2=0在区间(0,1)内至少存在两个不同实根。分析:(1)证明方程有根，用零点定理;(2)证明导函数方程有根，利用原函数法构造辅助函数，再用中值定理: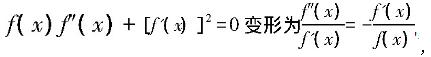，两边积分lnf'(x)=-lnf(x)+lnc，分离常数f(x)f'(x)=c，辅助函数即为F(x)=f(x)f'(x)。

证明:(1)由与极限的保号性可知，存在c∈(0,1)，使得f(c)<0。又f(1)>0，在[c,1]上用零点定理，至少存在一个η∈(c,1)，使得f(η)=0，即方程f(x)=0在区间(0,1)内至少存在一个实根。

(2)由函数f(x)在区间[0,1]上可导，从而一定连续，以及存在，得f(0)=0。由(1)得f(x)在区间[0，η]上满足罗尔定理条件，所以存在ξ∈(0，η)，使得f'(ξ)=0。令F(x)=f(x)f'(x)，显然F(0)=F(ξ)=F(η)=0。对函数F(x)分别在区间[0，ξ]及[ξ，η]上用罗尔定理得，至少存在两个不同的ξ1∈(0，ξ)及ξ2∈(ξ，η)，使得F'(ξ1)=F'(ξ2)=0，即f(ξ1)f″(ξ1)+[f'(ξ1)]2=0及f(ξ2)f″(ξ2)+[f'(ξ2)]2=0。因此，方程f(x)f″(x)+[f'(x)]2=0在区间(0,1)内至少存在两个不同实根。