城市犯罪不仅与社会、经济、地理环境等外部因素有关[1,2,3,4]，其内部还存在因果关系或目的关系[5,6]。探索城市犯罪事件之间的关联以及诱发因素，对认识犯罪、侦破案件、预防犯罪有着十分重要的作用，是当前公安部门的迫切需求。

灰色关联方法和时空关联模式挖掘方法是当前分析不同犯罪内部关联关系的主要手段。灰色关联方法根据多元犯罪在发展过程中的趋势一致性，量化多元犯罪间的相关度。如陈凯[7]使用灰色关联方法发现毒品犯罪与盗窃、抢劫犯罪事件具有强原因型关联机制，这种方法适用于分析多元犯罪动态历程的相似性，但难以揭示多元犯罪时空位置间的关联关系。时空关联模式挖掘是时空数据挖掘的重要组成内容[8,9,10]，可通过度量不同犯罪事件在邻近时空位置出现的频繁度，判别频繁度是否大于阈值，挖掘时空关联模式。代表性工作如Mohan等[11]基于空间邻近图挖掘多元犯罪事件以及酒吧、停车场等公共设施点间的局部空间同位模式，发现斗殴、盗窃犯罪事件易发生在酒吧地区；Celik[12]进一步考虑犯罪事件的时间属性，识别纵火、盗窃等犯罪事件频繁共生于多个时间切片的时空同现模式；Mohan等[13]在时空同现模式的基础上顾及犯罪事件的时间有序邻近提出了时空级联模式。这些模式可有效帮助相关部门发现犯罪吸引地和产生地。

分析发现，现有方法在模式筛选时依赖人为设置的频繁度阈值。当阈值设置不合理时，会导致挖掘结果遗漏真实模式，亦可能得到无意义的模式。因此，本文提出一种时空同现模式的非参数统计判别方法，该方法不依赖于人为设置的频繁度阈值，且无需对犯罪事件的时空分布模型进行假设，能够更加客观地揭示城市中多类犯罪事件的时空同现规律。

1、时空同现模式非参数统计判别

1.1研究策略

不同类型地理事件由于存在某共同的诱导因素，在邻近时空位置频繁出现，形成时空同现模式[14]。公共安全领域中，多类城市犯罪事件易因具有相似的诱导环境形成时空同现模式，例如毒品犯罪和诈骗犯罪均以获取钱财为目的，频繁发生在宾馆、娱乐场所[15]。现有通过设定频繁阈值识别时空同现模式的方法由于阈值设置的主观性，可能造成挖掘结果的误判以及漏判。例如，图1(a）中A类事件随机分布，B类事件聚集分布，两类事件同现频率较高。然而，随机事件的产生不受物理环境、社会环境以及人类活动的影响[16]，因此候选模式{A,B}为偶然发生的无意义模式。本文方法旨在发现由于多类事件间或潜在因子的诱导性相关而产生的时空同现模式，如图1(b）中，由于A、B两类事件间诱导关系，两类事件频繁聚集分布于相近的时空位置，进而形成有效的时空同现模式。

图1虚假模式和有效模式示例

本文运用显著性检验的思想，评价候选时空同现模式显著性，提出多元犯罪事件时空分布相互独立的零假设，若候选同现模式频繁度显著高于零假设下的频繁度，则将该候选模式判别为显著时空同现模式。

图2为本文研究策略框架，主要包括两个关键步骤。

图2研究策略框架

1）多元犯罪事件独立分布的零模型构建：对每类犯罪事件的时空特征（如空间自相关性）进行定量描述，分别独立产生保持观测数据集中各类犯罪事件时空分布特征的模拟数据集，从而构建满足零假设的零模型。

2）基于显著性检验的时空同现模式判别：针对每个候选模式，计算参与其中的各类犯罪事件在大量模拟数据集中同现的频繁度，得到该候选模式频繁度的试验分布；判别观测数据集中该候选模式频繁度的显著性。

1.2多元犯罪事件独立分布的零模型构建

为了构建多元犯罪事件时空分布相互独立的零模型，需要针对每类犯罪事件fi分别生成模拟数据。实际情况中，犯罪事件具有时空自相关性，如街头抢劫犯罪在道路流通性较好的区域具有明显的聚集现象，且在较偏僻路段集中发生在夜晚。因此生成模拟数据时，需要保持每类犯罪事件的自相关性特征。本文基于模式重建策略[17]，构建每类犯罪事件fi的模拟数据，主要包括两个步骤。首先采用时空统计量中的时空K函数、时空最邻近分布函数（G函数）、时空空隙函数（F函数）刻画犯罪事件fi的观测数据集（observationdataset,OD）的时空分布特征[18,19]；然后根据OD与模拟数据集（simulationdataset,SD）时空分布特征的差异构建目标函数，通过不断优化目标函数，逐步生成更加接近fi的观测数据集分布特征的模拟数据集。该方法可具体描述如下：

1）采用上述3个时空统计量刻画OD的时空分布特征χmOD(u,v)(m=1,2,3），其中u、v分别表示犯罪事件fi中的多个案件点间的空间和时间邻近半径；m=1,2,3分别表示时空K统计量、时空邻近统计量、时空空隙统计量的编号；

2）在所研究的时空范围S×T中随机生成与犯罪事件fi观测数据集OD中案件点数相同的初始模拟数据集SDh(h=0），其中h表示当前迭代次数；

3）计算第h次生成的模拟数据集SDh的时空统计量χmSDh(u,v)(m=1,2,3);

4）计算观测数据集OD与模拟数据集SDh时空分布特征的差异E(OD,SDh），表达为：

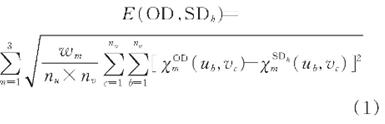
式中，ub表示第b个空间半径；vc表示第c个时间半径；nu和nv分别表示空间和时间半径的数量；wm为调节系数，用于均衡不同时空统计量在零模型构建中的重要性；

5）在时空范围S×T中随机生成一个案件点，并与SDh中任意一点进行替换，生成模拟数据集SDh+1。若E(OD,SDh+1)<E(OD,SDh），则接受SDh+1，返回步骤3），否则再次执行本步骤；

6）当E(OD,SDh）小于一个较小的阈值ε（实验中设为0.005）或者h达到最大迭代次数H（实验中设为80000）时，则输出SDh，终止循环。

进一步，采用上述方法对每个犯罪事件生成N组模拟数据集，完成零模型构建。

本文将以图3(a）中某事件的观测数据集为例，阐述其模拟数据（图3(b））的生成过程。首先计算OD的时空分布特征，如图3(c）的网格曲面。按照上述方法最终生成图3(b）所示的模拟数据SD，其时空分布特征的计算结果如图3(c）的灰色曲面。可以发现，模拟数据能够较好地保持观测数据集的时空分布特征。

1.3基于显著性检验的时空同现模式判别

本文进一步借助显著性检验思想，选取候选时空同现模式参与率作为检验统计量，判断多元独立分布的零假设是否成立。具体地，首先给定观测数据集OD，根据上述构建的零模型生成N组（实验中设为99）保持观测数据集中犯罪事件时空分布的模拟数据集{SD1,SD2,SD3…SDN}。然后对候选时空同现模式CP={f1,f2,f3…fk}，在观测数据集和模拟数据集中计算每类犯罪事件fi的参与率。记观测数据集中fi类犯罪事件的参与率为CPROD(fi,CP），记模拟数据集SDj中fi类犯罪事件的参与率为CPRjSD(fi,CP)。最后，判断候选时空同现模式CP的显著性，计算式为：

给定显著性水平α（实验中设为0.05），若p<α，则将候选模式CP识别为显著时空同现模式。

式（2）中，CPR用于度量某类犯罪事件在候选时空同现模式中出现的频率，计算步骤如下：

1）定义空间和时间半径，构建多元犯罪事件案件点间的时空邻近关系；

2）将k类犯罪事件f1,f2,f3…fk案件点中满足时空邻近关系的集合识别为候选时空同现模式CP={f1,f2,f3…fk}的实例，记为e(CP);

3）计算该候选时空同现模式CP中每类犯罪事件fi的参与率，表达式为：

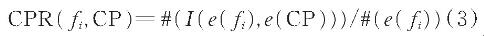
式中，等式右边分子表示犯罪事件fi的案件点是候选时空同现模式CP实例的成员的个数；分母表示犯罪事件fi的案件点数量。

采用图4所示数据集，阐述在候选时空同现模式CP={A,B,C}中3类犯罪事件参与率的计算过程。A、B、C分别有6、4、2个案件点，候选时空同现模式CP={A,B,C}具有3个实例{A1,B1,C1}，{A6,B1,C1}，{A2,B2,C2}。候选模式的每个实例中各类犯罪事件案件点两两之间均满足时空邻近关系。A的3个案件点参与到候选时空同现模式CP={A,B,C}中，则CPR(A,CP)=3/6；同理CPR(B,CP)=2/4,CPR(C,CP)=2/2。

图3多元犯罪事件独立分布零模型构建示意图

图4时空同现模式示意图

2、实验分析与应用

本文首先设计包含预设时空同现模式的4组模拟数据，验证本文方法的可行性，并与现有需要设定频繁阈值的CSTPM方法进行比较分析[13]。进一步地，对我国S市2016年的实际犯罪数据进行应用分析，探索S市中多类犯罪事件间的时空同现模式，以辅助S市公安事件的防控预警。

2.1模拟实验

为了验证本文方法识别时空同现模式和剔除虚假模式的有效性，采用3组包含虚假模式的模拟数据集和1组包含预设模式的模拟数据集进行测试。每组数据集中均包含A、B两类事件，空间研究域为[0,60]×[0,60]，时间研究域为[0,50]，时空分布如图5所示，图中“#”号意义同式（3）。

图5模拟数据集

4组模拟实验中，利用CSTPM方法得到候选时空同现模式{A,B}参与指数（co-occurrencepatternsindex,CPI）（即模式中各类事件参与率的最小值）的计算结果，同本文方法结果一起列于表1。下文将具体分析和比较两个方法在不同数据集中的实验结果。

数据集D1：如图5(a）所示，事件A、B在研究区域中呈随机分布。由于两类事件的案件点较多，故两类事件在邻近时空域中出现的频率较高（参与指数CPI为0.54）。在CSTPM方法中，若设置小于0.54的CPI阈值，则将该模式误判为时空同现模式。但此时本文方法能发现零假设下76%的数据集中事件A、B的参与率不小于D1中两类事件的参与率，因此接受零假设，判别候选时空同现模式{A,B}为虚假模式。

表1模拟数据集中时空同现模式{A,B}的方法对比结果

注：Y表示{A,B}为时空同现模式，N表示{A,B}不是时空同现模式

数据集D2：如图5(b）所示，两类事件生成过程相互独立，事件A呈随机分布，事件B呈聚集分布。由于事件B的时空簇在研究区域中占据较大空间，导致事件B时空簇中同时出现大量随机分布的A类事件，两类事件的同现频率较高（参与指数CPI为0.56）。在CSTPM方法中，若将CPI阈值设置为0.56以下，则该模式被识别为时空同现模式。然而，此时本文方法发现，零假设下依然能够很大概率地（0.85）得到大于或等于观测值的参与率，故对该虚假的时空同现模式进行有效剔除。

数据集D3：如图5(c）所示，独立生成100个呈聚集分布的A、B两类事件的案件点，两类事件不具有时空诱导性相关，故不存在时空同现关系。但是，两类事件的时空簇数目较多，二者的时空簇在研究区域内发生随机碰撞，进而导致时空同现模式{A,B}的频繁度较高（参与指数CPI为0.55）。只有当CPI阈值设置足够大时，现有方法才能有效过滤该虚假模式。本文方法发现二者的时空簇之间并不存在依赖关系，零假设成立，进而可以有效剔除该虚假模式。

数据集D4：如图5(d）所示，生成同时包含A类和B类事件的时空簇（时空半径为6），使得二者具有时空依赖关系，对两类事件分别增加若干噪声簇和噪声点，以削弱二者间的时空同现频率（参与指数CPI为0.30）。当CPI阈值设置较小时，CSTPM方法中难以发现该模式。而本文方法能发现零假设下大于或等于数据集D4中两类事件参与率的情况是一个小概率事件，故拒绝零假设，将候选时空同现模式判别为显著时空同现模式。

分析上述4组实验，可以发现本文方法不仅可以有效识别多类事件的时空同现模式，而且可以剔除由单类事件时空分布特征造成的虚假时空同现模式。

2.2实际应用

本文将经济发达的长江三角洲城市群中某市S作为研究区域，随着该市城镇化率的提高，大量流动人口涌入城市，增加了社会不安定因素，导致该市犯罪活动频发、多样。因此本文对该市2016年犯罪数据进行应用分析，首先从原始数据中剔除时空信息记录缺失的数据，最终保留年犯罪案件数目大于200的犯罪事件，可总结归纳为13类犯罪事件：诈骗（9318个）、盗窃民宅（7532个）、盗窃电动车（5643个）、吸毒（3872个）、扒窃（2223个）、赌博（1824个）、盗窃车内财物（1376个）、盗窃商店（1291个）、扰乱治安（1092个）、盗窃自行车（650个）、盗窃单位（515个）、盗窃摩托车（413个）和伤害（264个）。

犯罪事件间时空同现模式具有尺度依赖特征，随着分析尺度（即时空半径）的不同，不同类别犯罪事件会形成不同的时空同现模式。例如微观尺度上，餐饮区域傍晚就餐人流量大，钱财和货物汇聚，从而吸引嫌疑人产生财产犯罪（如抢劫、盗窃）[20,21]；中观尺度上，财产犯罪（如抢劫、诈骗）在下午易聚集发生在具有高度复合功能的商业中心区域[22,23]。因此，采用单一分析尺度难以准确描述多元犯罪事件间的同现规律。实验中，在[500,3000]m×[1,7]d的范围内，以500m和1d为步长，共设置42组时空半径进行分析。若候选时空同现模式在多个时空半径下被识别为显著模式，则表明该模式中不同犯罪事件间呈现牢固的同现规律，依据该模式可以进一步帮助公安部门制定针对性犯罪打击策略，提高打击犯罪效率。由于篇幅有限，图6和图7列举了本文方法和CSTPM方法在多个时空半径下对部分时空同现模式的评价结果。分析结果可以发现，本文方法在较小分析尺度上主要发现扒窃与室外盗窃以及吸毒与赌博的时空同现模式；在较大分析尺度上主要发现吸毒与诈骗以及赌博、伤害与扰乱治安的时空同现模式。本文方法通过候选时空同现模式频繁度的试验分布对该模式进行评价，无需人为设置频繁度阈值，降低了现有方法的主观性。若将CPI阈值设置为0.3，在CSTPM方法中仅能在较大分析尺度上得到时空同现模式，在较小分析尺度上均很难发现有效的时空同现模式。因此本文方法较CSTPM方法有一定优越性。

图6部分时空同现模式的p值热点图（本文方法）

以时空同现模式{扰乱治安，盗窃电动自行车，扒窃}为例，对两种方法的实验结果进行比较分析。该模式集中发生在S市主城区，具体地，在较小分析尺度（1000m×3d）上，主要分布在中小学校、餐饮店、超市、商场、公园等公共设施点附近；在较大分析尺度（2000m×5d）上，主要分布在建筑物类型较多的中央商业区域。但是，盗窃电动自行车的案件点数量明显高于另外两类犯罪的案件点数量，使得在3类犯罪事件同现区域外依然存在大量盗窃电动自行车的案件点，进而导致该模式的参与指数CPI在多个时空半径下普遍偏小（如图8所示）。

图7部分时空同现模式的CPI值（CSTPM方法）

图8示例模式CPI分布

若将CPI阈值设置为0.3,CSTPM方法仅能在11个较大分析尺度下发现该模式；本文方法发现3类犯罪事件在中小尺度上、多个时空半径下（1500m×3d）均能构成显著的时空同现模式，如图9所示，可以发现3类犯罪事件在零假设下的同现频率难以达到观测数据集中的参与率。

进一步，以分析尺度1500m×3d为例，分析该模式的时间分布，如图10所示，可以发现6月—9月期间每日07:00—09:00、18:00—20:00和1月—2月期间每日09:00—12:00是该模式的高发时间段。下面结合公共设施的空间分布，对犯罪时空同现模式在3个时间段的形成进行解释。

图9零假设下示例模式中3类犯罪参与率分布（“★”表示观测参与率）

1)07:00—09:00(6月—9月）。从图11(a）可以发现，该时段内同现模式实例点主要发生于中小学校和超市附近，图12(a）中的Cross(K）函数[24]表明该模式与两类POI(pointofinterest）具有显著空间依赖关系。进一步采用基于LDA(latentDirichletallocation）模型的关键词抽取方法[25]分析该时段内的案件点的文本记录，发现扒窃、盗窃电动车两类犯罪分别约有51%、53%的记录具有“防范意识低”“视野遮挡”“人多”“混乱”等关于防范意识及人流量的词语。结合文本记录及破窗理论[26]发现中小学校、超市每天具有早高峰期[27,28]，该时间段的人流使得治安环境混乱，为扒窃和盗窃电动车创造了有利条件，使得3类犯罪同现。对此，建议该时段在学校、超市附近加强治安管理以保证社会秩序，从而减少扒窃、盗窃电动车嫌疑人浑水摸鱼、趁乱作案的可能。

图10示例模式时间分布

2)18:00—20:00(6月—9月）。分析图11(b）中示例模式实例点及公园等娱乐场所、商铺和餐饮店的空间分布，可以发现二者均呈现由南向北的分布，模式实例点密度随设施点的稀疏变小；图12(b）表明，在空间上，该模式与上述公共设施具有显著依赖关系。分析该时段内案件点的文本记录，发现扒窃、盗窃电动车两类犯罪分别约有57%、51%的记录具有“防范意识低”“视野遮挡”“人多”“混乱”等关于防范意识及人流量的词语。理性选择犯罪理论指出，“犯罪嫌疑人根据环境采取策略，从而以最小的代价得到最大的价值”[29]。而上述区域人员流动较频繁，且钱款、财物较集中[28]，保安及巡逻人员难以全面管理，犯罪嫌疑人实施犯罪行为时难以察觉，从而使得上述场所容易同时滋生3类犯罪。对此，建议在娱乐场所、沿街商铺和餐饮区域加强巡逻，提醒市民保护好随时物品，从而保持人与人的空间距离，减少冲突。

图11在3个时间段中示例模式实例点及POI分布

图12在3个时间段中示例模式实例点与POI的Cross-K函数值

3)09:00—12:00(1月—2月）。分析图11(c）发现，示例模式实例点空间分布与超市、商场相似，并且模式实例点密度高的区域设施点较为集中，且图12(c）表明超市、商场对该模式的空间分布具有一定诱导性。进一步，结合本文记录分析发现，该时段内扰乱治安、扒窃、盗窃电动自行车3类犯罪分别有约54%、53%、55%的记录具有“采买”“购物”“促销”“碰撞/摩擦”“没注意/察觉”“随意停放”等关于春节出行采购及钱财防范疏忽的词语。分析其文本记录的详细内容，发现春节期间大量市民携带钱财在超市、商场进行购物，市民注意力集中在挑选商品上，难以形成守望效应，使得超市、商场区域成为滋养3类犯罪的有利土壤。对此，建议超市、商场在春节前后增加保安人员，及时协调群众纠纷，并对另外两类犯罪嫌疑人起到威慑作用，从而减少该模式的发生。

3、结语

现有城市犯罪时空关联分析过程依赖于人为设定的参数，容易导致结果存在偏差甚至错误。本文结合时空统计学提出一种时空同现模式非参数检验的方法，有利于对多元犯罪事件时空同现模式的有效性进行客观评价，进而揭示不同犯罪事件形成环境的相似性。通过对模拟数据和我国长江三角洲城市群中S市2016年犯罪数据进行实验分析，得出以下结论。

1）本文方法能够顾及单类犯罪事件自相关特征对多类犯罪事件时空同现模式的影响，有效识别具有统计意义的显著时空同现模式；

2）犯罪事件时空同现模式具有明显的尺度依赖性。扒窃与室外盗窃、吸毒与赌博的时空同现模式主要发现于较小分析尺度；吸毒与诈骗、赌博、伤害与扰乱治安的时空同现模式主要发现于较大分析尺度；

3）具有相似建成环境和社会环境的犯罪事件易形成时空同现模式。例如，夏季和春节期间频繁的市民活动使得时空同现模式{扰乱治安，盗窃电动自行车，扒窃}在人流量大的区域频发，该模式的形成机理与日常活动理论的观点相符。

本文研究数据为S市公安部门接警数据，犯罪事件的实际案发时间与接警时间可能存在差异，需要进一步顾及犯罪事件案发时间的不确定性，以提高犯罪时空同现模式识别的准确率。同时，现实城市中犯罪事件所依赖的建成环境与社会环境均具有时空异质特征，导致犯罪时空同现模式亦存在区域分异特点，需要发展异质环境下城市犯罪时空同现模式的挖掘方法。

参考文献：

[2]王增利,刘学军,陆娟,等.犯罪网络构建及其时空分析——以入室盗窃为例[J].武汉大学学报·信息科学版,2018,43(5):759-765)

[4]李卫红,闻磊,陈业滨.改进的GA-BP神经网络模型在财产犯罪预测中的应用[J].武汉大学学报·信息科学版,2017,42(8):1110-1116,1171.

[5]杨子良.论关联犯罪[J].中国刑事法杂志,2000,46(4):13-22.

[7]陈凯.基于灰色关联分析法的毒品犯罪群实证研究——以湘潭市雨湖区判决资料为样本[D].湘潭:湘潭大学,2010.

[8]李德仁,王树良,李德毅,等.论空间数据挖掘和知识发现的理论和方法[J].武汉大学学报·信息科学版,2002,27(3):221-233.

[9]李德仁,王树良,史文中,等.论空间数据挖掘和知识发现[J].武汉大学学报·信息科学版,2001,26(6):491-499)

[10]刘大有,陈慧灵,齐红,等.时空数据挖掘研究进展[J].计算机研究与发展,2013,50(2):225-239)

[15]田兴洪,姚桂华.论毒品犯罪与其他犯罪的关联性[J].云南警官学院学报,2004,2(2):53-55)

[21]龙冬平,柳林,冯嘉欣,等.社区环境对入室盗窃和室外盗窃影响的对比分析——以ZG市ZH半岛为例[J].地理学报,2017,72(2):341-355)

[23]柳林,张春霞,冯嘉欣,等.ZG市诈骗犯罪的时空分布与影响因素[J].地理学报,2017,72(2):315-328)

[27]高悦尔,陈小鸿,李佳,等.中小城市义务教育阶段学生上下学出行特征研究[J].长安大学学报(社会科学版),2016,18(3):104-108)

[28]宋广文,肖露子,周素红,等.居民日常活动对扒窃警情时空格局的影响[J].地理学报,2017,72(2):356-367)

陈袁芳,蔡建南,刘启亮,邓敏,张雪英.城市犯罪时空同现模式的非参数检验方法[J].武汉大学学报(信息科学版),2019,44(12):1883-1892.

基金:国家自然科学基金(41730105);国家重点研发计划(2016YFB0502303);中南大学研究生自主探索创新项目(2017zzts346);公安部科技强警基础工作专项(2016GABJC43);江苏省高校自然科学研究重大项目(15KJA420002).