首页 >
论文范文 >
自然科学论文 >
数学论文 >
几何论文 >
试论序列映射与极限映射之间关于几乎周期性和逐点周期跟踪性的关系
摘要：在强一致收敛条件下研究了序列映射与极限映射之间关于几乎周期性和逐点周期跟踪性的关系,所得结果对强一致收敛下几乎周期点和逐点周期跟踪性理论的发展有一定的促进作用．
加入收藏
一致收敛是拓扑动力系统中的重要概念．众所周知，只有少数序列函数的性质在一致收敛条件可以被遗传到极限函数，例如连续性、黎曼积分、不动点等；很多动力学性质在一致收敛的情况下并不能被遗传到极限函数，例如拓扑传递[1]、拓扑混合[2]、初值敏感性[3]等．为了研究序列函数和极限函数之间的动力学关系，文献[4]给出比一致收敛更强的条件，即强一致收敛，从此很多学者在强一致收敛条件下开始研究序列函数和极限函数之间的动力学性质，得到了丰硕的成果[5,6,7,8,9,10,11,12,13,14]．例如文献[5]证明了在强一致收敛下度量G-空间中，若序列函数是拓扑混合，则极限函数也是拓扑混合的；文献[6]给出序列函数是渐进周期的，在强一致收敛下，其极限函数也是渐进周期的；文献[7]证明了在强一致收敛下是W(f）的子集；文献[8]证明了在强一致收敛下是AP(f）的子集．
本文在文献[8]的基础上，继续研究几乎周期点，得到如下结果：（1）设序列映射{fn}强一致收敛于等度连续映射f且点列{xk}是每个映射fn的几乎周期点．若，则x是f的几乎周期点．（2）若序列映射{fn}强一致收敛于等度连续映射f，则limsupAP(fn）AP(f），从而改进和推广了文献[8]的结论．另外本文还研究了强一致收敛下跟踪性的动力学性质，得到：若序列映射{fn}强一致收敛于f且fn具有Fine逐点周期跟踪性，则f具有逐点周期跟踪性．这些结果对强一致收敛下几乎周期点和逐点周期跟踪性理论的发展有一定的促进作用．
1、基本概念
定义1设（X,d）是度量空间，对任意的n∈N+,fn:X→X连续，f:X→X连续．称序列映射{fn}在X上强一致收敛于f，如果
d(fnm(x),fm(x））<ε．
记作
定义2设（X,d）是度量空间，f:X→X连续，x∈X．若对任意包含x的开集U，存在正整数m>0，对任意的正整数k>0，⁆r∈（k,k+m]使fr(x）∈U，则称x是f的几乎周期点．f的几乎周期点集用AP(f）表示．
定义3设（X,d）是度量空间，f:X→X连续，点x∈X．若存在m>0使fm(x)=x，则称x为f的周期点．f的周期点集用P(f）表示．
定义4设（X,d）是度量空间，f:X→X连续．若对任意的ε>0，存在δ>0，当d(x,y）<δ时，∀m≥0，有
d(fm(x),fm(y））<ε，
则称f是等度连续．
定义5设（X,d）是度量空间，f:X→X连续，δ>0，{xi}i≥0是X中的序列．若对任意的i≥0，有d(f(xi),xi+1）<δ，且存在n>0使得xkn+j=xj,0≤k,0≤j<n，则称{xi}i≥0是X的δ-周期伪轨．
定义6设（X,d）是度量空间，f:X→X连续，ε>0,y∈X，{xi}i≥0是X中的序列．若对任意的i≥0，有d(fi(y),xi）<ε，则称yε-跟踪{xi}i≥0.
定义7设（X,d）是度量空间，f:X→X连续．若对任意的ε>0，存在δ>0，使得当{xi}i≥0是X中f的δ-周期伪轨时，存在y∈P(f），存在n∈N,yε-跟踪{xi}∞i=n，则称f具有逐点周期跟踪性．
定义8设（X,d）是度量空间，f:X→X连续．若对任意的ε>0，使得当{xi}i≥0是f的ε-周期伪轨{xi}i≥0，存在y∈P(f），存在n∈N,yε-跟踪{xi}∞i=n，则称f具有Fine逐点周期跟踪性．
2、主要结果
引理1[8]设（X,d）是度量空间，对任意的n∈N+,fn:X→X连续，f:X→X连续，序列映射{fn}强一致收敛于f,x∈X．若x是每个映射fn的几乎周期点，则x是f的几乎周期点．
定理1设（X,d）是度量空间，对任意的n∈N+,fn:X→X连续，f:X→X等度连续，序列映射{fn}强一致收敛于f．若点列{xk}是每个映射fn的几乎周期点且，则x是f的几乎周期点．
证明由f的等度连续性知，∀ε>0，0<δ<ε/3，当d(z1,z2）<δ时，∀l≥0，有
由知，对上面δ>0，存在正整数m>0使d(xm,x）<δ．由（1）式知，l≥0，有
由引理1可知，xm是f的几乎周期点，从而对，存在正整数N>0，对任意的整数q≥0，，使得
由（2)—(3）式知
因此x是f的几乎周期点．
定理2设（X,d）是度量空间，对任意的n∈N+,fn:X→X连续，f:X→X等度连续．若序列映射{fn}强一致收敛于f，则limsupAP(fn）⊂AP(f).
设z∈limsupAP(fn），则存在m>N1，使
取y∈AP(fm）∩B(z，δ）．由y∈AP(fm）知，对，存在正整数N2>0，对任意的整数q≥0，r∈（q,q+N2]，使得
由y∈B(z，δ）和（4）式，
由（5)—(7）式知
故z∈AP(f），则
注1下面举例说明即使满足定理2的条件，也推不出limsupAP(fn)=AP(f).
例设I=[0,1]，对n∈N+，定义fn:X→X,
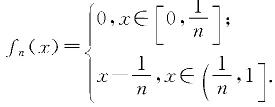
定义f:X→X,
f(x)=x,x∈[0,1].
依此类推，若，其中0≤i≤n-1，则存在m=m(n,x）∈N+，当k≥m时，有
fnk(x)=0.
定理3设（X,d）是度量空间，对任意的n∈N+,fn:X→X连续，f:X→X连续，序列映射{fn}强一致收敛于f．若fn具有Fine逐点周期跟踪性，则f具有逐点周期跟踪性．
证明∀ε>0，取0<δ<ε/3．设{xi}i≥0是f的δ-周期伪轨，则∀i≥0，有
由知，对上面δ>0，存在正整数N1，当n>N1时，l≥0，y∈X，有
取m>N1并固定m，由（10）式知，当i≥0时，有
由（9）和（11）式，当i≥0时，有
由fm具有Fine逐点周期跟踪性知，，存在n∈N，当i≥n时，有
由（10）式知，当i≥n时，有
d(fmi(x),fi(x））<δ．
因此，当i≥n时，有
d(fi(x),xi)<d(fi(x),fmi(x))+d(fmi(x),xi）<ε．
下面证明x∈P(f）．由x∈P(fm）知，存在k>0使得fmk(x)=x．由（10）式知，
d(fmk(x),fk(x））<δ．
故
d(fk(x),x)<(fk(x),fmk(x))+(fmk(x),x）<ε．
由ε任意性，fk(x)=x，故x∈P(f），因此f具有逐点周期跟踪性．
3、总结
本文在强一致收敛下，研究了序列映射与极限映射关于逐点周期跟踪性的关系，得到若fn具有Fine逐点周期跟踪性，则f具有逐点周期跟踪性；另外还研究了序列映射与极限映射在几乎周期性方面的关系，笔者通过证明得到如下结果：
(1）点列{xk}是每个映射fn的几乎周期点且，则x是f的几乎周期点；
参考文献：
[2]曾凡平,严可颂,刘新和.强一致收敛与动力性质[J].广西大学学报(自然科学版),2008,33(3):305-309.
[3]王良平.强一致收敛下的初值敏感性与等度连续性[J].浙江大学学报(理学版),2012,39(3):270-272.
[5]冀占江.度量G-空间中强一致收敛条件下混合性的研究[J].数学的实践与认识,2018,48(11):237-240.
[6]邓晓霞,金渝光.强一致收敛下的保持性和混沌性[J].西南师范大学学报(自然科学版),2014,39(2):31-34.
[7]王良平.一致收敛下极限系统回复性的研究[J].广西师范学院学报(自然科学版),2010,27(4):12-16.
[8]秦斌,严可颂,徐雪群.一致收敛下极限系统的传递性研究[J].广西师范学院学报(自然科学版),2009,26(3):10-14.
[9]罗飞,金渝光.强一致收敛条件下序列系统与极限系统的关联性[J].重庆师范大学学报(自然科学版),2015,32(4):78-80.
[10]杨忠选,尹建东.映射列一致收敛与敏感依赖性[J].南昌大学学报(工科版),2013,35(4):385-391.
[13]向伟杰,金渝光.强一致收敛下的Li-Yorke混沌和分布混沌[J].重庆师范大学学报(自然科学版),2018,35(2):93-97.
[14]罗飞,金渝光,白丹莹.强一致收敛条件下的集值Devaney混沌性[J].西南大学学报(自然科学版),2015,37(2):79-83.
冀占江,张更容.强一致收敛下几乎周期点和逐点周期跟踪性的动力学性质[J].东北师大学报(自然科学版),2020,52(02):30-34.
基金:国家自然科学基金资助项目(11461002);湖南省自然科学基金资助项目(2018JJ2074);广西自然科学基金资助项目(2018JJB170034);广西高校中青年教师科研基础能力提升项目(2019KY0681).
分享：
优化问题具有非常重要的实际应用价值，备受研究者们关注。二层规划因其上、下层决策变量互相影响制约、结构非凸、非处处可微等几何特性使其求解难度较大。越来越多的人们把智能优化算法应用于二层规划寻优问题中，从而产生了很多新型算法。在诸多智能优化算法中，蚁群算法(AntColonyAlgorithm）因其具有自组织和正反馈等特点，在解决优化问题时备受研究者青睐。
2020-12-02
1、空间解析几何教学改革初探与实践2、基于k细分等几何层次模型的多重网格算法研究3、Tesla阀性能的影响因素及其优化分析4、笛卡尔关于科学研究统一性的数学构想5、AZ31镁合金双曲率方杯拉深成形的有限元分析及工艺优化6、惯性定理的几何意义7、探讨矩阵行列式几何意义的应用
2020-08-11
双曲抛物面在几何学中有其特殊的性质,它是由直线运动所产生的曲面;同一族的任意两条直母线异面;它的任意一条直线都与另一族直线所有的直线相交;对双曲抛物面上的任意一点,两族直母线中各有一条直母线经过该点,正是因为这些特性使得它在实际生活方面有着广泛的应用。
2020-07-13
教师在中职立体几何教学中运用信息化工具，能更好地帮助学生掌握立体几何问题的解题思路，有效提升学生的空间想象能力和抽象思维能力。在使用信息化工具时，教师需要细致地处理好各个教学环节中信息化工具的定位、使用时机、流程细节等，还要及时反思和优化。作为新时代的教师，把信息技术的理念和工具积极且合理地加入到立体几何的课堂教学中。
2020-07-09
随着计算机编程教学的不断深入,教师在实际的教学过程中往往会遇到很多的问题,学生对于几何编程都非常感兴趣,却不知道从何入手,学生们反复强调实际学习效果不佳,主要原因在于几何编程操作方法简单,但是随着几何图形设计任务的增加,对于学生的计算机思维能力的要求也逐步提升,因此要求教师在这个过程中应当关注学生的分解以及递归思维能力的培养。
2020-07-09
子空间是点集拓扑学中的重要概念,它既可以拓展拓扑学的研究范围,也可以帮助我们建立不同拓扑空间之间的联系,而且很多重要的概念,比如,连通子集、紧致子集等都是通过它来定义的,所以掌握好这一概念对后续的学习十分关键.笔者在十余年的教学实践中发现,虽然子空间的定义和相关性质在内容上比较简单,但是这并不代表它可以很容易地灵活运用.
2020-07-09
椭圆与圆很相似。就像把画圆的工具称作圆规一样，画椭圆的工具称作椭圆规。 椭圆规的构造：由有十字形滑槽的底板和旋杆组成(如图1)。在十字形滑槽上各装有一个活动滑标。滑标下面有一根旋杆。此旋杆与纵横两个滑标连成一体。移动滑标，其下面的旋杆能作360°旋动，画出符合椭圆方程的椭圆。
2020-07-09
通过培养学生的几何空间思维能力和逻辑推理能力，提高学生学习课程的基本方法，掌握科研创新的方法和能力。笔者结合最新的课程改革基本理念和多年的教学实践，总结经验，潜心思考，对现今出现的课堂效果较差、学习兴趣逐渐减弱等现象进行了深入探讨和研究，提出了以下几点浅薄的看法。
2020-07-09
勾股定理也称毕达哥拉斯(Pythagoras)定理,是数学中非常重要的定理之一。毕达哥拉斯是公元前6世纪希腊著名的数学家和哲学家,在西方,他被普遍认为是该定理最早的证明者,因此勾股定理就以他的名字命名。然而早在公元前1700年,古巴比伦人就发现已这一定理,无独有偶,最迟公元前1105年,我国的商高便能利用一般的“弦图”来证明这一定理。
2020-07-09
相对微分几何是关于仿射空间中超曲面的一种理论,包含等积几何和中心仿射几何为其特例.设x:MA是从n维连通定向流形M到n+1维仿射空间A的局部强凸浸入.设{Y,y}是x(M)的相对法化.3-形式C是最重要的几何不变量之一.Simon3-形式C˜定义为3-形式C的无迹部分。
2020-07-09
人气：6027
人气：3169
人气：3023
人气：2628
人气：2543
我要评论
期刊名称：数学的实践与认识
期刊人气：2783
主管单位：中国科学院
主办单位：中国科学院数学与系统科学研究院
出版地方：北京
专业分类：科学
国际刊号：1000-0984
国内刊号：11-2018/O1
邮发代号：2-809
创刊时间：1971年
发行周期：半月刊
期刊开本：16开
见刊时间：1年以上
影响因子：0.553
影响因子：0.322
影响因子：0.352
影响因子：0.000
影响因子：0.000
科普杂志阅读、期刊信息查询、论文下载、文献查询、原创文章检测等多项服务。
服务热线
您的论文已提交，我们会尽快联系您，请耐心等待！
你的密码已发送到您的邮箱，请查看！
2020-07-09
353
上传者：管理员
