在全基因组关联研究（GWAS）中，群体分层导致了检测统计量的膨胀增加了关联检测的假阳性率，从而降低了对数量性状核苷酸（QTNs）检测的统计效力，它通常用个体在亚群中的比例表示[1,2,3,4]。基于家系数据的GWAS分析所关注的家系内的信息不受分层影响，因为同一个家系内遗传和非遗传等位基因都具有共同的遗传祖先[5,6,7,8]。在非基于家系的关联分析研究中，普遍使用全基因组遗传标记计算出的主成分（PCs）分析方法矫正群体分层的影响[9,10]。主成分分析（PCA）的GWAS虽然只包括前几个主成分带来的群体分层混淆效应，它通过亲缘关系矩阵模拟个体间的遗传协方差，所以这种矫正方法可以被认为是主成分在表型值上的回归[11,12,13,14,15,16,17]。在实际应用基于主成分分析的GWAS过程中，即使因为利用固定效应模型的协变量数只包含了前几个主成分，即使这几个主成分不和样本数在同一个数量级，也仍然保持了合理的统计效力[18]，群体分层效应可以在使用相关主成分较少的主成分分析的GWAS模型中得到很好的纠正[19,20]。

间断性状如复杂疾病，抗病和异常行为是基因定位的重要目标性状，尽管这类可遗传的性状表型值由二进制或不连续的数字表示，但它们的遗传并不能通过简单的孟德尔遗传解释，基因定位时同样应考虑除检测标记外的群体分层，家系结构和亲缘相关性[21,22]。许多动植物的这类性状可以以数量性状的形式定量统计和描述，例如玉米对赤霉素感染的抗性可以用接种节间感染面积占总面积的比例表示，而水稻对稻瘟病菌感染的抗性则通过病损植株的数目占总植株的比例表示。然而大部分二元响应变量的性状无法定量表示这类性状，与正态分布的数量性状用剩余误差作为矫正的表型不同，由于间断性状的自变量和因变量之间的尺度不同，无法简单估计疾病表型的剩余误差，这就需要将广义线性模型（GLM）中的logit回归用于这类性状的全基因组关联分析。即使校正了一些临床固定效应协变量，logit回归仍然和简单线性回归一样会受到群体分层导致检验统计量的膨胀的影响。PLINK1.9是一个被广泛使用分析复杂疾病数据软件，虽然1.9版本的PLINK绝大多数情况都是分析数据高效而稳定，但当使用上百个主成分矫正分层时，计算速度大大下降；同时PLINK在水平很多的分类协变量时，需要转换为多个二进制虚变量，这也无形的增加了需要同时分析的协变量数目。最后如果分析的协变量和表型值之间相关极大时，PLINK的回归模型中协变量的回归系数会远大于1，这导致标记的效应的估计值降低。针对这些问题描述了一种Logit回归能够同时修正大量协变量的高效算法，我们扩展了PLINK功能，让它可以高速实现。

1、材料和方法

1.1材料

试验数据群体研究的核心包括Wellcome Trust Case Control Consortium(WTCCC）的4种疾病，有：冠心病、类风湿性关节炎、一型糖尿病和二型糖尿病。每一种疾病的病例样本都是从英国各地随机选择的人群。这些试验的控制组有两个来源：1500份是1958年英国出生队列的代表性样本，1500份是英国联邦三大国家血液服务机构招募的献血者。其中总样本包含3950人，其中2415名男性，1535名女性，1594名患病个体和2356名对照个体。经过质量控制，关联分析了313518个SNP。

模拟的基因型数据集是来自康奈尔大学的2468株玉米群体，经过质量控制后有300000SNP位点，模拟由对系谱中的每个个体，在一定长度的染色体片段上，按照重组率生成中等密度和高密度的遗传标记基因型，同时，在给定多个QTL或标记的位置和对数量性状的效应值、剩余多基因、永久环境和误差方差组分的条件下，随机产生个体目标性状的表型值。由于试验主要研究在QTNs的位置和遗传效应发生变化时，新方法的性能如何在每一轮的模拟过程中，模拟基因组遗传力固定为0.8不变，保持固定的样本发病率比例为50%,QTN的数目分别设定为20个、200个和2000个三个水平，不同数目的QTNs被随机地放置在模拟基因组的全部多态SNP上，而且从形状和尺度参数分别为1.66和0.4的伽马分布中，随机抽取每个模拟QTN的遗传效应。

1.2方法

1.2.1基因组广义线性模型

根据广义线性模型理论，连接函数建立起了疾病性状表型向量y和被检验标记效应的关系：

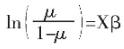
这就是二岐性状基因组logit回归模型。其中，μ是每个个体疾病性状的平均值组成的向量，β是固定效应向量，包含被检验标记的遗传效应βSNP;X是由β所对应的系数矩阵。

在μ=Xβ处，对似然函数进行二阶泰勒展开并化简为：

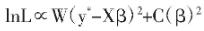
根据迭代重加权最小二乘法估计回归系数的估计值向量β：

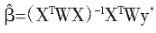
和正态随机变量的误差方差σe2:

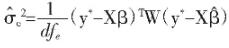
其中，dfe是误差自由度，W=μ（1-μ）是权重，y*=lnμμ1-μμ+y-μμ（1-μ）是由表型值y和回归系数组成的新的因变量。

采用推断卡方统计量，推断SNP与疾病性状关联：

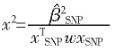
此处，xSNPβ赞SNP是被检验标记的回归项，这个统计量服从自由度为1的卡方分布。

1.2.2考虑多个协变量快速基因组广义线性模型

考虑群体分层时，通常以亲缘关系矩阵的前i个特征向量U1∶i作为logit模型的协变量去矫正由群体分层导致的分层效应，基因组广义线性模型变为：

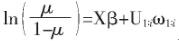
由于特征向量间相互独立，每一个协变量的回归系数可以分别估计为ω赞1∶i。不像正态分布的数量性状那样用剩余误差作为矫正的表型，因为自变量和因变量之间的尺度不同无法估计疾病表型的剩余误差。因此，我们把U1∶iω赞1∶i作为已知的协变量，只需要用y*-U1∶iω赞1∶i去代替y*后，再利用广义线性模型估计每个SNP的遗传效应和标准误。

1.2.3复杂群体分层的快速矫正步骤

由于每个主成分是之间是相互独立的，我们可以使用分别求解出每个加权主成分对应的分层效应值ω赞1∶i，计算U1∶iω赞1∶i作为一个已知的协变量。我们提供两种扩展方式：

（1）基于PLINK，利用PLINK软件自身的协变量回归算法，这时几百个协变量回归模型等价转化成单个协变量回归模型。

（2）扩展PLINK，用y*-U1∶iω赞1∶i作为表型直接估计每个SNP的遗传效应和标准误，这种情况不需要再重新求解协变量的回归系数，更为准确，尤其适合协变量和表型值相关较大（如估计育种值）时使用，由于需要对PLINK软件重新编译，我们暂用R语言编程实现。

1.2.4主成分选择标准

为了综合评价几种方法的优劣性，以及比较优化基因组控制的广义线性混合模型主成分回归法自身的稳健性，对于统计特性评价采用如下两个标准验证：

（1）基因组控制效果：通过全基因组统计量的平均卡方值控制值（gc值）接近1的程度，并结合Q-Q图和理论线的偏离程度判断基因组数据中存在的群体分层的校正效果。

（2）QTL检测个数：同一群体，不存在明显的假阳性的条件下，以Bonferroni阈值为标准比较QTN的检测个数。

2、结果与分析

2.1模拟结果

模拟方法包括4种：直接运行PLINK的GLM模型算法，PLINK自带的矫正PC协变量的GLM模型算法（PLINK-PCs），基于PLINK矫正PC协变量的GLM模型算法（Bs-PLINK-PCs）和扩展PLINK矫正PC协变量的GLM模型算法（Ex-PLINK-PCs）。从图1上半部分的Q-Q图可以看出直接运行PLINK的GLM模型算法的黄色线明显从起始位置就开始上扬，并且平均基因组控制值分别等于1.94,1.71和1.69，这两点表明群体内存在明显的群体分层需要矫正。而后三种方法的QQ图几乎完全一致的重合且前端都很好的贴合理论线，基因组控制值也都在1附近，这说明这几种方法均没有出现明显的假阳性或者假阴性。在检测效力上除了在模拟20个QTNs时扩展PLINK矫正PC协变量的GLM模型算法（ExPLINK-PCs）的蓝色会有极其微小的提高外其他情况三种方法均完全重合，这说明了只采用主成分作为协变量时，我们提出的两种方案均可以替代PLINK自带的矫正PC协变量的GLM模型算法，且在只有主成分作为协变量时，我们提出的两种方案结果也几乎没有差别。

图1使用玉米基因组模拟100轮后2种方法表现的Q-Q图和QTNs检测效力图，其中黄色代表直接运行PLINK的GLM模型算法，绿色代表基于PLINK矫正PC协变量的GLM模型算法（Bs-PLINK-PCs）。

2.2实际资料结果

表1为五种方法在4组数据的基因组控制值的比较，从表1中可看出：无论是哪个群体，在不放任何协变量的广义线性回归模型的基因组控制值均大于1，这表明各个群体中都有一定的群体分层现象存在，这一现象导致了统计量的膨胀。同时随着引入的主成分协变量增多，基因组控制值逐渐降低，群体分层的影响也逐渐变小，但是无论是将1个，5个还是10个主成分作为协变量都无法完全的矫正统计量的膨胀，然而当主成分协变量的数目增多到200个时，基因组控制值达到1左右，良好的矫正了群体分层效应。由于前4种方法的检验统计量造成的假阳性，检测到的潜在QTN不具有可比性，所以只比较200个主成分作为协变量的广义线性模型回归QTN检测能力，见表2。

表1五种方法的基因组在4组数据的基因组控制值

注：CAD代表冠状动脉粥样硬化性心脏病疾病群体；RA代表类风湿关节炎群体；T1D代表一型糖尿病群体；T2D代表二型糖尿病群体。

表2基于PLINK矫正PC协变量的GLM模型算法在4组数据定位p值超过阈值潜在QTN的个数

2.2.1冠状动脉粥样硬化性心脏病疾病群体（CAD）结果

在冠状动脉粥样硬化性心脏病疾病群体中，采用200个PC作为协变量明显的矫正了检验统计量的膨胀，这令我们的结果的基因组控制值十分接近1。

2.2.2类风湿关节炎（RA）结果

类风湿关节炎群体中，检验统计量膨胀不如冠状动脉粥样硬化性心脏病疾病群体明显，但是采用10个主成分作为协变量仍然无法完全矫正群体分层，采用200个主成分作为协变量虽然矫正了检验统计量的膨胀，但基因组控制值为0.9997，略低于1有假阴性趋势，可能进一步需要减少主成分的个数，可能影响潜在QTN总数。

2.2.3一型糖尿病（T1D）结果

一型糖尿病群体结果和类风湿性关节炎群体类似，统计量都是只存在略微的膨胀，这令200个PC作为协变量的基因组控制值收缩到0.9975。

2.2.4二型糖尿病（T2D）结果

二型糖尿病群体统计量膨胀适中，采用200个主成分在4个群体中的基因组控制值为0.9999，最接近1。

图2使用广义线性模型法分析冠状动脉粥样硬化性心脏病疾病群体时的统计量膨胀在Q-Q图上的体现，左图为右图浅红色区域的放大

图3冠状动脉粥样硬化性心脏病疾病使用200个主成分作为协变量的GLM模型法的曼哈顿图与Q-Q图

图4使用广义线性模型法分析类风湿关节炎疾病群体时的统计量膨胀在Q-Q图上的体现，左图为右图浅红色区域的放大

图5类风湿关节炎疾病使用200个主成分作为协变量的GLM模型

图6使用广义线性模型法分析一型糖尿病疾病群体时的统计量膨胀在Q-Q图上的体现，左图为右图浅红色区域的放大

图7一型糖尿病疾病使用200个主成分作为协变量的GLM模型的曼哈顿图与Q-Q图

图8使用广义线性模型法分析二型糖尿病疾病群体时的统计量膨胀在Q-Q图上的体现，左图为右图浅红色区域的放大

图9二型糖尿病疾病使用200个主成分作为协变量的GLM模型的曼哈顿图与Q-Q图

2.2.5计算时间和内存消耗比较

这里借助PLINK软件分析比较了使用直接使用PLINK软件进行广义线性模型分析，在已知主成分的情况下，使用PLINK软件自带的功能进行同时考虑100个和200个主成分作为协变量的广义线性模型分析，经过我们拓展的考虑200个主成分作为协变量的广义线性模型分析在同等情况下：IntelCorei5-8350U1.70GHz,16GBRAM的个人笔记本电脑上比较使计算所需时间和软件运行峰值所占用的内存。这里其中总样本包含3950人，关联分析了313518个SNP。由表3可知，无论何种情况，使用广义线性模型所需的内存均不大，并且使用PLINK自带的考虑主成分作为协变量的广义线性模型分析时，随着同时考虑的主成分增加，虽然内存占用没有增多，但方法所需时间会随之大大增加。新方法即使同时考虑200个协变量，速度也和不考虑任何协变量的PLINK广义线性模型速度和内存差别不大，比PLINK自带功能速度快200多倍。因为底层程序逻辑不同，R语言的程序慢于C语言编写的PLINK软件，所以表中没有对比这种方案和PLINK软件的速度。

表3不同方法在关联分析3950人的313518个SNP所需的计算时间和峰值内存

3、讨论

通过以上的研究，展示了快速的广义线性模型的主成分回归法可以很好的矫正关联分析中的群体分层，结果显示无论是评价指标中的Q-Q图还是基因组控制值，都显示只要考虑作为协变量的主成分数目恰当，就可以很好地控制全基因组关联分析中的假阳性。提出的两种方法检测到的QTNs都几乎一致等于PLINK自带方法，并且方法在实际测试中分析200个PCs作为协变量时，速度最多比PLINK快200倍以上。人类的实际数据分析结果中有两组数据的基因组控制值都略低于1，导致这种情况的原因可能是一致的选择200个主成分作为协变量，但是不同群体的所需矫正的主成分协变量数目与群体本身有关，所以200个主成分并非是所有群体的最优的主成分数目。在后续的研究中可以以研究不同群体矫正群体分层的最优主成分数目为目标再拓展该方法的实用性。方法虽然借助PLINK软件，但是保持PLINK计算内存消耗不大的优势下，又比其自带多协变量回归速度上也极大提高。同时主成分是实现亲缘关系矩阵普分解得到的特征向量，实现亲缘关系矩阵的计算方法有很多，在后续研究中亲缘关系矩阵计算上也可以寻求简化算法。同时从模拟中发现，提出的两种方案在仅仅包含主成分作为协变量时差别不大，这是由于主成分和表型值间的关系不大，但是假如协变量和表型值间的回归系数远大于1时会极大的影响QTNs的检测效力。提出的第二种方案现在慢于PLINK软件，但是并非算法不简捷，相反的少求解一个回归系数会令方程更简单，所以这种方法如果扩展到PLINK的快速回归计算中，不但会比用R语言编写的程序计算效率更高，理论上会比PLINK软件本身的速度进一步提高。在日后的研究里，可以尝试适当扩大整体样本数，这可以增加结果的精确程度。同时，也可以尝试对方法进行改良和优化，期望新方法可以在不同群体中都选择最合适的主成分数目。

4、结论

1.9版本的PLINK也是一个通常用于研究疾病对照试验基因定位的工具，在性能和兼容性方面有了显著的改进，虽然它可以纠正数百个协变量，也可以纠正来自多级分类协变量的虚变量，但随着协变量数目增加到一定数目，扫描的速度也会大大降低。在此基础上拓展了PLINK软件，让它同时快速的修正大量协变量去矫正关联分析中存在的群体分层，极大地提高了间断性状广义线性模型全基因组关联分析的运算效率，操作简单方便，易于理解。

参考文献：

[7]李冰,田丰昊,褚慧慧,等.基于模糊数学方法的延吉市生态系统健康评价[J].延边大学农学学报,2015,37(3):188-195.

[23]王艳.矩阵指数的计算[J].黑龙江八一农垦大学学报,2010,22(4):85-88.

张敬言,宋禹昕,张姮妤,张莹,杨润清.间断性状关联分析中复杂群体分层的快速矫正[J].黑龙江八一农垦大学学报,2020,32(03):27-34+63.

基金:全基因组关联分析分层求解方法(C2018045).