首页 > 论文范文 > 自然科学论文 > 数学论文 > 代数论文 > 探讨MATLAB在线性代数教学中的应用

探讨MATLAB在线性代数教学中的应用

2020-03-27 442 上传者：管理员

摘要：本文从MATLAB和线性代数教学的融合的必要性出发，基于二者间可行性的结合点进行了探索，总结和分析二者融合过程中存在的困难及问题，对在线性代数教材和教学过程MATLAB的应用细节进行了深入探讨。

关键词：
M ATLAB
实例求解
矩阵
线性代数
加入收藏

线性代数是普通高校理工科和经管类专业的一门重要的数学基础课程，也是众多领域中解决实际问题的重要数学工具。本文重点考虑如何将计算机技术引入线性代数的教材和教学过程[1]。若能将重要的数学软件引入线性代数的教学过程，任何多元线性方程组的求解都将不存在本质困难。学生得以抽离烦琐的计算过程，转而把精力集中放在对概念和理论的理解上，并且能够做到理论联系实际。

一、MATLAB与线性代数的有机结合

MATLAB与线性代数的有机结合可以体现在很多具体的方面，根据理工科专业线性代数的具体教学内容，在这里着重强调以下几个重要方面。

1. 行列式的计算。按照行列式的定义，n阶行列式的计算所需进行的乘法次数为（n-1）×n次。实际工程问题中所遇到的矩阵阶数通常在几十到几百之间，因而，矩阵行列式的定义通常只能用于理论推导，无法用于具体计算。即便提高计算机性能也是杯水车薪，本质上需要发展并改进算法，然后再把行列式的计算问题交给计算机去完成。为此，可通过引入MATLAB后，按以下方式来展开对行列式的教学。

（1）低阶行列式的笔算技巧。根据行列式的类型（数字型、含参型、抽象型）和具体特征，行列式的计算方法有很多，具体包括：定义法、性质法、降阶法、三角化法、递推法、公式法、加边法、数学归纳法等。在教学过程中，为加强学生对行列式定义及相关性质的理解，可选择性地向学生介绍其中的部分方法。对于低阶（4阶及其以下）行列式，要求学生能够通过上述方法完成对这些行列式的笔算过程。

（2）高阶行列式的MATLAB计算方法。用MATLAB来进行行列式的计算属于数学理论和工程实际的结合问题。技巧性太强的计算方法往往只适合手工计算而不适合计算机计算。因此，MATLAB所使用的计算行列式的方法是三角化法。具体的操作步骤包括：①用行列式为1的初等矩阵进行初等变换；②将主对角线下方的元素全部打成0；③计算对角元素的乘积。按照上述方法，MATLAB给出了直接计算方阵行列式的函数det.m，其调用格式为：D=det（A）该函数的输入A为任意的方阵，输出D即为该矩阵的行列式。根据上述三角化法的具体操作步骤，可对MAT-LAB的行列式算法det.m的计算复杂度和计算时间进行大致估计。对任意的n阶方阵，待消元的元素个数为（n-1）2/2个，每消除一个元素需要对一行元素进行乘法和加法运算。精确分析后得出，消掉一个元素平均需要进行2n/3次乘法，因而整个消元过程所需的乘法次数为:

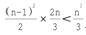
以n=25阶的行列式计算为例，使用消元法所需的乘法次数大约是5000次，比定义法所需的乘法次数减小了近1023倍。若使用每秒能做一万亿（1012）乘法运算的计算机进行运算，则仅需5×10-9s。即便是n=500阶的行列式，乘法次数也不超过4×107次，因而计算时间不超过10-4s，这样的运算速度在工程实际中是完全可以接受的。

2. 特征值和特征向量的计算。特征值和特征向量在动力系统的设计和求解等工程实际问题中有着广泛的运用。根据其定义和性质，矩阵A的特征值和特征向量的计算方法如下：

（1）计算特征多项式f（λ）=|λE-A|。这一步往往需要计算一个含参的高阶行列式，计算量很大。

（2）求特征值，也即求出特征方程f（λ）=0的全部根λ1，λ2，…，λn。这一步本质上需要求解一个一元n次方程，当n≤4时可通过求根公式进行求解，当n≥5时往往很难求解。

（3）求特征值所对应的特征向量，也即求每个λ1所对应的齐次线性方程组（λ1E-A）x=0的非零解。对于四阶以上的矩阵，上述步骤都很难通过手工计算完成。正确的做法是先从理论上研究特征值和特征向量的性质，在此基础上，学习并讨论特征值和特征向量的MATLAB算法。

为此，可在教材和教学过程中引入对该算法的介绍。MATLAB提供了实现上述特征值和特征向量计算方法中三个步骤的对应函数，具体形式如下：

（1）用函数f=ploy（A）计算A的特征多项式的系数向量f。

（2）用函数lamda=roots（f）计算特征方程的全部根，并表示为列向量。

（3）用函数p=null（lamda*I-A）算出对应的齐次线性方程组的基础解系p，将所有基础解系所包含的特征向量拼在一起就是A的特征向量矩阵。不仅如此，实际上MATLAB已经对上述步骤进行了集成，仅需一个调用函数eig.m就可以直接求出矩阵A特征值和特征向量，该函数的调用方式为：[p，lamda]=eig（A），其中，输出变量lamda代表A的特征值作为对角元素所构成的对角矩阵，输出变量p代表A的特征向量作为列向量所拼成的矩阵。

3. 矩阵的行最简形的计算。使用消元法求解线性方程组时，需通过初等变换将相应的增广矩阵打成行阶梯型或者行最简型。根据增广矩阵的行阶梯型的特点，可以判断原方程组是适定的、欠定的或者不相容的。在此基础上，可进一步完成对方程组的求解。然而，对于一般的n元线性方程组，将增广矩阵打成阶梯型需要进行的乘法次数约等于n3/3次，利用回代法进行求解时需要进行的乘法次数约等于n2/2次。当n很大时，与n3/3相比，回代次数n2/2可以忽略不计，因而可近似认为用消元法求解线性方程组所需的乘法次数为n3/3。照此估计，处理十元线性方程组就需要进行近400次乘法运算，这是手工运算所不能接受的。因而，处理实际工程问题时，必须借助MATLAB等数学工具完成将增广矩阵打成阶梯型的过程。MATLAB将“行最简型”的计算过程集成为一个名为rref.m的调用函数，其调用格式为：[U0，ip]=rref（[A，b]），其中，输出变量U0代表输入增广矩阵[A，b]对应的行最简型，输出变量ip代表该行最简型的首非零元所在列的列标。

二、关于将MATLAB引入线性代数教学的几点思考

将MATLAB引入线性代数教材和教学过程的好处自不待言，然而，在教学实践中通常会出现以下具体困难。

1. 讲解线性代数时，需要学生有一定的MATLAB基础，可考虑在线性代数的讲解中穿插一部分必要的MATLAB知识。本质上，线性代数用到的只是部分初级MATLAB知识，即其中的矩阵代数部分。完成这部分MATLAB基础知识的讲解仅需3—4个课时。

2. 为使学生对空间的概念有形象的认识，可充分利用MATLAB的绘图模块，这就需要用到解析几何的某些基础知识，这一需求高中解析几何便可满足。

3. 不同专业学生对线性代数的需求层次不同，针对这一差异，教材和教学内容可考虑采用由浅入深的模块式结构：

（1）第一个模块（也即初级模块）主要围绕求解线性方程组展开。

（2）第二个模块（中级模块）主要围绕向量空间、特征值和特征向量展开。

（3）第三个模块（高级模块）主要围绕应用线性代数解决实际问题展开。

将MATLAB引入线性代数教材和教学过程，可以摈弃线性代数问题求解中大量烦琐的计算过程，集中培养学生的抽象思维能力和解决实际问题的能力。MATLAB的绘图模块可使得线性代数的抽象性大大减弱，适用性大大增强，从而使得学生对知识点的理解更为深入，并且能够灵活掌握知识点的应用方法。充分借鉴国外已有的研究经验，以MATLAB辅助线性代数教学工作，改变线性代数教学“繁、难”的现状，是大力提升教学效果的可行途径。如何具体实现MATLAB与线性代数教学的有机结合，切实做到两者间的协调统一、互相促进，尚有很多值得进一步探讨的问题，也是后续教材编写和教学改进值得关注的重点方向。

参考文献：

[1]陈怀琛,龚杰民,线性代数实践及MATLAB入门[M].北京:电子工业出版社,2005.

蔚涛,周薛雪.MATLAB与线性代数教学的有机结合[J].教育教学论坛,2020(2):267-268.