
摘要:本文主要目的是在monoidalHom-Hopf代数情形中引入偏模余作用,并考虑其整体化问题,对Hom-模余代数整体化特性进行了论证。
 加入收藏
加入收藏
偏群作用最初由Exel[1]在研究算子代数时引入的,作为强有力的工具用来研究由Hilbert空间上的偏等距算子生成的C*-代数.作为偏群作用的推广,Caenepeel和Janssen[2]在2008年引入了偏Hopf作用及余作用,为Hopf代数研究注入新的生机和活力,已成为一个重要的研究方向.近年来,在偏Hopf作用方面已经取得许多重要结果[3-8].
Hom-代数的概念是由Makhlouf和Silvestrov介绍[9],随后引起学者们对Hom-代数的研究.Caenepeel和Goyvaerts[10]从范畴角度重新定义Hom-双代数、Hom-Hopf代数,并且将其重新命名为monoidalHom-双代数、MonoidalHom-Hopf代数.很多Hopf代数上的经典的结果都可以推广到monoidalHom-Hopf代数上[11-14].
本文主要目的是在monoidalHom-Hopf代数情形中引入偏模余作用,并考虑其整体化问题.假设K为一个域.本文所讨论的代数、余代数、模及余模均在域K上考虑.所有的映射都是K-线性映射.本文总假设H为一个Hopf代数,对于其余乘法 ,继续使用Sweedler符号
,继续使用Sweedler符号 ,这里省略和符号∑.欲了解更多有关MonoidalHom-Hopf代数的知识,请参阅文献[10-14].
,这里省略和符号∑.欲了解更多有关MonoidalHom-Hopf代数的知识,请参阅文献[10-14].
1、主要结果
本节主要引入偏Hom-模余代数的概念,并给出从Hom-模余代数出发构造偏Hom-模余代数的过程.定义1设(H,β)是一个monoidalHom-Hopf代数,(C,γ)是一个monoidalHom-余代数,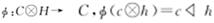 是一个线性映射且满足兼容条件
是一个线性映射且满足兼容条件 .称(C,γ)为一个右偏(H,β)-Hom-模余代数,若对任意c∈C,h,k∈H满足下列条件:
.称(C,γ)为一个右偏(H,β)-Hom-模余代数,若对任意c∈C,h,k∈H满足下列条件:
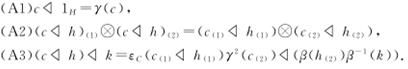
如果εC(c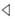 h)=εC(c)εH(h),条件(A3)变为
h)=εC(c)εH(h),条件(A3)变为 ,此时的偏(H,β)-Hom-模余代数就变成(H,β)-Hom-模余代数.现在我们将要从Hom-模余代数出发,去构造偏Hom-模余代数.
,此时的偏(H,β)-Hom-模余代数就变成(H,β)-Hom-模余代数.现在我们将要从Hom-模余代数出发,去构造偏Hom-模余代数.
设(D,η)是一个右(H,β)-Hom-模余代数,其上的模结构映射为:令(C,η)是(D,η)的子monoidalHom-余代数.由于(D,η)具有Hom-模结构,这样可以考虑把(D,η)的Hom-模作用限制到(C,η)上,以此来得到偏Hom-模作用.但是观察到C◁H的象不一定在C中,所以需要再把这个象投射到C中去.令π:D→C为(D,η)到(C,η)的投射,且满足ηπ=πη.考虑映射为了使得到的“ ”是(H,β)在(C,η)上的右偏Hom-作用,需要探索一些必不可少的条件.
”是(H,β)在(C,η)上的右偏Hom-作用,需要探索一些必不可少的条件.
即验证了条件(A3)成立.在上面的假设条件下,我们就得到了右偏(H,β)-Hom-模余代数(C,η),称之为诱导出来的右偏(H,αH)-Hom-模余代数.下面,将给出偏Hom-模余代数的整体化定义.定义2设(H,β)是一个monoidalHom-Hopf代数,(C,η)是一个右偏(H,β)-Hom-模余代数.(C,η)的一个整体化是四元素(D,γ,θ,π),其中(D,γ)是一个模作用为“1111”的右(H,β)-Hom-模余代数,θ:C→D是一个monoidalHom-余代数单同态,π是从(D,γ)到(θ(C),γ)的余乘法投射,并满足下列条件:77777下面,给出本节的主要结论.定理1设(H,β)是一个monoidalHom-Hopf代数,则任何偏(H,β)-Hom-模余代数都存在整体化.证明设(C,η)是一个右偏(H,β)-Hom-模余代数,其上的模结构映射为:

 ,显然,θ是一个单射.
,显然,θ是一个单射.

下面来证明(C H,η
H,η β,θ,π)是(C,η)的整体化.需要验证定义中条件(1)-(3)成立.这里,只验证(1),其余条件可以类似验证.至于条件(1),事实上,
β,θ,π)是(C,η)的整体化.需要验证定义中条件(1)-(3)成立.这里,只验证(1),其余条件可以类似验证.至于条件(1),事实上,
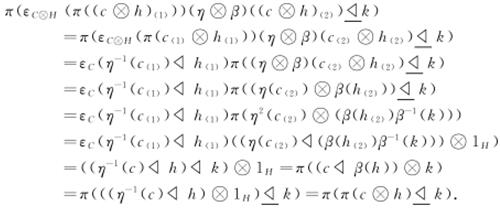
成文静,郭怀文,陈全国.偏Hom-模余代数的整体化[J].曲阜师范大学学报:自然科学版,2020,46(1):1-3.
分享:

1、基于核心素养视角的线性代数教学改革研究与实践2、三角形网格上形态开闭算子的研究3、浅谈线性代数教学中的直觉思维的培养4、工科数学课程群建设5、培养综合应用能力的离散数学教学改革研究6、疫情期间线性代数课程线上教学模式探索7、线性代数课程应用能力的培养途径和方法研究——以软件工程专业的教学实践为例8、基于独立学院的高等代数教学研究
2020-08-11
“线性代数”是工科类本科生的专业基础课程,其主要处理线性关系问题。课程的内容主要包括基础概念—行列式、矩阵及其运算;基本变换—矩阵的初等变换与线性方程组,向量组的线性相关性;以及线性问题分析—相似矩阵及二次型等内容。采用MATLAB解决矩阵特征值问题的相关教学实践论文已有报道[3],此外,将微课应用到线性代数的教学中也取得了良好的效果[4]。
2020-08-10
独立学院,也常称为独立二级学院,是由公办普通本科院校与社会力量联合举办的相对独立的二级学院.独立学院数量众多,招生人数众多,招生录取分数线普遍较低.为了适应社会发展对人才的需求,绝大多数独立学院的人才培养定位为“应用型”人才.在开办之初,很多独立学院是照搬母体高校的课程体系和教学模式,但是由于独立学院学生的基础较母体高校的学生之间存在着较大差异,教学上很难达到独立学院人才培养的要求,其中数学课程教学中出现的问题尤为突出.
2020-08-10
2020年春季学期,哈尔滨理工大学线性代数课程网络教学如期开课,哈尔滨理工大学理学院数学系线性代数课程教学团队结合学习通平台、微信群和腾讯QQ与学生保持互动学习,并建立基于网络、手机、电脑的教学新模式,基于学校自建课程进行混合式教学,立足本校学生学情和需要,使线上线下的混合式教学很好地衔接。教学模式信息化的改革,增添了教学活力,促进了教学互动,并且较高效率地完成教学任务,达到了教学大纲要求的教学效果。
2020-08-10
外汇储备作为我国关键形式的储备资产,同时又是我国基础货币投放的主要渠道。自1994年我国实行以市场供求为基础、有管理的浮动汇率制度以来,我国外汇储备规模大幅扩大,从2006年开始,我国外汇储备规模位列世界第一,外汇储备的增加有提升国家声誉,吸引外商投资和拉动国民经济等积极影响。
2020-08-04
在线性代数教学中,求矩阵的幂、判定矩阵对角化、求解特征值的反问题、判定矩阵合同关系以及判定实二次型的正定性等问题都可以借助于矩阵特征值与特征向量实现。本文对这些问题进行了归纳与分析,以便学生能够熟练掌握求矩阵特征值与特征向量的方法,熟悉特征值与特征向量在线性代数教学中的应用。
2020-06-28
数学作为工科院校的一门基础课,对学生学好专业课起着至关重要的作用。通常情况下,工科院校开设的数学课程主要包括高等数学、概率与数理统计、线性代数、积分变换等,在这些课程中,普遍存在“教师难教,学生难学的现象,特别是线性代数,表现得更为突出。文章从教师的教学策略和学生的学习方法两个方面提出了工科线性代数教学策略。
2020-06-28
目前,关于连续函数空间中基于框架的构造、性质、函数空间刻画及其在信息处理中的应用已经得到了完善与发展。然而,在实际应用中,由于输入/输出数据和滤波器都是离散的,所以基于框架的算法实现都是在数字环境中完成的。基于数字的框架又名为离散空间中的框架,并不一定能够通过连续环境中的框架离散化得到,即使可以得到,也必须附加许多条件。
2020-06-28
众所周知,代数闭域K上的Sylvester矩阵方程AX-XB=C有唯一解当且仅当矩阵A和矩阵B无公共特征向量。为深入讨论,利用Sylvester算子研究了Sylvester矩阵方程在任意域K上的可解性,得到其有唯一解当且仅当A和B的特征多项式无公共素因式的结论。在Sylvester矩阵方程有解的情况下,给出了其多项式解。
2020-06-28
广义柔度矩阵可利用低阶模态参数近似表示,因此受到广泛关注.本文基于广义柔度矩阵引入广义模态柔度矩阵,利用Nelson方法计算其对损伤参数的敏感性.本文提出的损伤定位方法,相比于现有方法,在振型数据不完整及含有噪声的情况下,该方法具有使用模态参数少,定位的损伤单元数比实际损伤单元数略多且不遗漏损伤单元等特点.
2020-06-28
人气:4575

人气:3590

人气:3369

人气:3124

人气:2972
我要评论

期刊名称:数学进展
期刊人气:3703
主管单位:中国科学协术协会
主办单位:中国数学会
出版地方:北京
专业分类:科学
国际刊号:1000-0917
国内刊号:11-2312/O1
邮发代号:2-503
创刊时间:1955年
发行周期:双月刊
期刊开本:16开
见刊时间:一年半以上


影响因子:0.553

影响因子:0.322

影响因子:0.352

影响因子:0.000

影响因子:0.000
您的论文已提交,我们会尽快联系您,请耐心等待!
你的密码已发送到您的邮箱,请查看!