首页 > 论文范文 > 自然科学论文 > 数学论文 > 数理逻辑论文 > 探究数学建模中MATLAB的运用

探究数学建模中MATLAB的运用

2020-07-10 437 上传者：管理员

摘要：全国大学生数学建模竞赛是高校竞赛排行榜中的重要竞赛。因此,从数学建模的步骤出发,介绍MATLAB的基本功能,并通过具体的实例讨论MATLAB在数学建模中的应用。

关键词：
Matlab
建模竞赛
数学建模
数据拟合
数理逻辑
线性规划
加入收藏

随着科学技术的高速发展,自然科学的各个领域都需要在调查研究的基础上建立数学模型,并通过计算解决实际问题。数学建模在合理假设的基础上将实际问题简单化、抽象化,用数学知识解决问题并接受实践的检验。在这一过程中,问题的求解需要借助计算机计算才能完成。MATLAB作为应用最广泛的科学计算软件,具有强大的数据处理、数据分析及图像可视化等功能。在每年的全国大学生数学建模竞赛中,MATLAB是普遍应用的软件。本文就MATLAB在数学建模中的应用进行简单介绍。

1、MATLAB在数学建模中的应用

1.1MATLAB基本功能介绍

全国大学生数学建模竞赛创办于1992年,每年举行,是高校学科竞赛排行榜的基础竞赛之一。数学建模的主要步骤为模型准备,根据实际对象的特征进行模型假设,建立正确的数学模型,选择恰当的方法进行模型求解,进一步分析模型并进行模型检验和推广。在数学建模过程中,需要阐述建模思路,对所得结果进行数学分析,根据获取的资料对模型参数进行计算求解。模型求解时,MATLAB最常用的软件。

MATLAB具有强大的数值计算能力,集数值分析、矩阵计算、可视化以及编程能力、交互性等诸多强大功能于一体,并具备强大的绘图功能,语句可读性强,易掌握。学生在参加大学生数学建模竞赛前,要对MATLAB的基本功能有基本了解,每队队员至少需要提前用2个月的时间掌握MATLAB的数据处理、二维三维绘图、MATLAB编程以及各种工具箱,并针对常用的数学模型进行MATLAB编程,才能在数学建模竞赛时熟练应用MATLAB。下面给出MATLAB在数学建模中的两个简单应用。

1.2MATLAB数据拟合

数据处理是数学建模的基础,对于题目给定的或采集到的数据进行处理和分析,将其转换成数学表达式从而建立模型时,通常用到的是数据插值和拟合。给定一批数据点,若要求所求曲线(曲面)通过所有数据点,是插值问题;若不要求曲线(曲面)通过所有数据点,而是要求它反映对象整体的变化趋势,是数据拟合。MATLAB提供了插值和拟合函数来得到相应的数学模型,下面给出一个曲线拟合的实例。

例1:已知观测点的数据如下:

求用三次多项式进行拟合的曲线方程,并将拟合后的函数图像与原始观测数据的图像画在一张图里进行比较。

解:本题是典型的曲线拟合问题,曲线拟合的目的是根据最小二乘原理,用较简单的函数逼近一个复杂的或未知的函数[1]。MATLAB曲线拟合可以采用多项式拟合、指定函数拟合等,本题采用三次多项式拟合,用MATLAB可以简单得到三次多项式拟合函数,具体语句如下:

通过MATLAB运行可知,本题用三次多项式拟合的函数为f(x)=2.3699x3+5.0105x2+2.9767x+1.9836。

图1给出了三次多项式拟合的函数图像,并与原始点进行了比较。可见,用MATLAB对已知数据进行拟合易实现,因此建模竞赛以及实际问题中得到了广泛应用。

图1三次多项式拟合

图1三次多项式拟合下载原图

1.3MATLAB线性规划

规划类问题是常见的数学建模问题。MATLAB提供强大的规划模型求解命令,可以简单快速地计算出所要的结果。MATLAB规划模型包括线性规划、整数规划以及非线性规划等[2]。MATLAB线性规划的基本函数为linprog,非线性规划的函数命令为fmincon。

在生产实践中经常会遇到用现有资源安排生产从而取得最大经济效益等问题,线性规划问题是根据实际问题分析决策变量,建立目标函数,给出约束条件,进而求解规划问题[3]。线性规划的目标函数一般是求最值,可以是最大值也可以是最小值,约束条件的不等号可以是小于号或大于号。为了便于格式统一,MATLAB规定线性规划的目标函数为求最小值,约束条件为小于等于号,因此对于最大值问题可以通过简单的数学转换化为求最小值问题。下面给出一个MATLAB线性规划的实例。

例2:求解线性规划问题

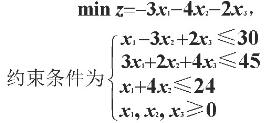
解:求解本题的MATLAB命令为:

MATLAB运行可知,最优解X=13.20002.70000.0000,即x1=13.2、x2=2.7、x3=0,于是最优值为50.4。

2、结语

熟练应用MATLAB可以让数学建模求解过程事半功倍。学生在准备数学建模竞赛时要自主学习,多看多记,自己动手编程,仔细体会程序设计思想,记住常用命令,才能更好地将MATLAB应用于建模分析和求解。同时,在平时数学建模课堂教学中,教师也可以将MATLAB引入教学,培养学生解决问题的能力,提高学生的创新意识,并将MATLAB应用于后续的专业课和工作中。

参考文献：

[1]卓金武.MATLAB在数学建模中的应用[M].北京:北京航空航天大学出版社,2013.

[2]余胜威.MATLAB数学建模经典案例实战[M].北京:清华大学出版社,2016.

[3]张志涌,杨祖樱.MATLAB教程[M].北京:北京航空航天大学出版社,2015.

武文佳.MATLAB在数学建模中的应用[J].现代制造技术与装备,2019(11):78-79.

基金:2018年上海电机学院重点课程《MATLAB基础与应用》建设项目资助(A1-0288-19-027-034-MATLAB基础与应用);2019年上海电机学院重点课程《微积分A》建设项目资助.