
摘要:为提高结构可靠性分析问题求解的稳定性和计算效率,提出一种基于乘子法的结构可靠性分析方法。该方法针对正态分布的独立随机变量,从结构可靠度问题的KT条件出发,结合拉格朗日函数,构造出了相应的增广目标函数,并利用外罚函数法进行求解和结构可靠性分析。数值算例和工程算例验证了该方法的稳定性和有效性。
 加入收藏
加入收藏
在工程设计中,材料不均匀、安装误差等问题的存在,往往会对结构性能造成各种影响甚至破坏。传统结构设计没有考虑施工过程中的不确定因素,而实际施工中载荷和材料性质等不断变化,这些不确定因素会使失效概率不断增大。为了确保产品的结构可靠性,有必要对不确定结构可靠度分析方法进行研究。目前,大量研究者为了解决实际工程问题,发展和提出了许多先进的计算方法[1,2,3,4,5,6]。徐强等[7]提出了大坝体系可靠度改进计算方法;黄逸群等[8]对实际工程问题中隧道型钢喷混凝土初期支护进行可靠度计算;高东川等[9]使用一次二阶矩理论中心点法预测了支护后的软岩巷道围岩的稳定性;肖宇峰[10]提出了一种基于子网同构判定的高效计算方法;李怀龙等[11]计算了轨道板横向宽轨枕单元的轨下截面和板中截面的可靠度;李奎等[12]研究了深埋隧道素混凝土衬砌可靠度计算模型,并进行了相关可靠性分析计算;王鹏等[13]提出了基于应力-强度模型的DTECS-2设备可靠度计算方法;Hamed Fazlollahtabara等[14]提出了一个用于可靠度计算的集成马尔可夫和反向传播神经网络。通过分析发现,乘子法在处理实际工程结构可靠性分析问题时具有较好的效果。
基于此,本文提出一种基于乘子法的结构可靠分析方法,该方法稳定有效地解决不确定结构可靠度指标求解问题,数值算例和工程实例验证了所提出的方法在解决可靠性分析问题时具有较好的稳定性和有效性。
1、乘子法理论介绍
在最优化理论中,罚函数法是求解约束优化问题的一个重要方法,把约束优化问题转化成一个或一系列的无约束优化问题,通过无约束问题来求解约束极值问题。通常采用的方法是在原目标函数加上一个“惩罚项”来迫使迭代点逼近可行域。通常情况下,必须使用罚参数与约束条件来构造惩罚项。当前迭代点不是可行点时,就要构建惩罚项,并且使得惩罚随着不可行点到可行域距离的增大而变大;可行点处不实施惩罚。惩罚项强制迭代点逼近可行域,最终落入可行域。外罚函数法结构简单,可以直接调用无约束优化算法的通用程序,但是也具有局限性,罚参数σk→+∞,会使得增广目标函数变得“越来越病态”。为了改善这种局限,在乘子法中引入拉格朗日函数,并加上适当的罚函数。Powell和Hestenes在1969年针对等式约束优化问题同时独立提出了乘子法,后来Rockfellar在1973年将乘子法推广到求解不等式约束优化问题。从原问题的拉格朗日函数出发,加上适当的罚函数,可以将原问题转化为一系列的无约束优化子问题。
对于等式约束问题,数学模型可以表示为:

其中,h(x)=[h1(x),h2(x),…,hl(x)]T,可行域D={x∈Rn|h(x)=0},拉格朗日函数为

其中,乘子向量λ=(λ1,λ2,λ3,…,λl)T。设问题(1)的KT点(局部极小点)是(x*,λ*),由最优性条件可得:
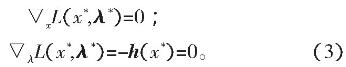
对于任意的x∈D,有

由式(4)可知,如果乘子向量λ*已知,则式(1)可转化为

使用外罚函数法求解,式(5)的增广目标函数为
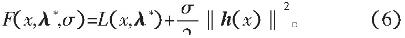
可以得出,当σ>0适当大时,x*是F(x,λ*,σ)的极小点。由于乘子λ*未知,可考虑增广目标函数

选取一个再适当改变λ的值,求得新的,直到得到满足要求的λ*和x*。具体地说,在第k次迭代求出无约束子问题minF(x,λk,σ)的极小点xk,极小值满足如下必要条件:

而在原问题的KT点(x*,λ*)处

为使{xk}→x*和{λk}→λ*,可取乘子序列{λk}。

当h(xk)→0时,λk+1→λk,{λk}收敛,而h(xk)=0时,(xk,λk)满足KT条件。
在结构可靠度分析中,结构可靠度指标β的几何意义是标准正态坐标系中原点到极限状态曲面的最短距离,垂足即为验算点,验算点到标准坐标系的原点的距离即为结构可靠度指标。
假设有n个独立的影响结构可靠度的非标准正态分布的随机变量,该结构的极限状态函数可表示为

设计验算点为xi*,通过X軒i*=(Xi*-μXi*)/σXi*对Xi*标准化之后,

通过优化处理可靠度指标才能确定验算点,先设β为极限状态曲面上点P∑X1,X2,…,Xn∑的函数,通过求得β2的最小值,进而得出β的最小值,便可得出验算点和可靠度指标的值。因此可得如下优化数学模型:

基于上述讨论,给定功能方程及其分布概型、随机变量的基本参数,即可通过迭代求解并得到可靠度指标,迭代计算步骤如下:
1)选取初始值。给定x0∈Rn,λ1∈Rl,σ1>0,0≤ε<<1,υ∈(0,1),η>1。令k:=1。
2)求解子问题。以xk-1为初始点,求解无约束子问题的极小点xk和可靠度指标βk:

3)检验终止条件。若‖h(xk)‖≤ε,停算,输出βk作为可靠度指标,xk作为近似极小点;否则,转步骤4)。
4)更新罚参数。若‖h(xk)‖≥υ‖h(xk-1)‖,令σk+1:=ησk;否则,σk+1:=σk。
5)更新乘子向量,令λk+1=λk-σkh(xk)。
6)令k:=k+1,转步骤2)。
2、可靠度算例
2.1数值算例
极限状态方程为

x1与x2相互独立,且均服从正态分布。变量分布参数取值如表1所示。根据本文方法,经过4次迭代,求得可靠度指标β=2.3302,迭代计算数据见表2。使用改进一次二阶矩(AFOSM)法检验,经过11次迭代,求得可靠度指标β=2.3302,迭代计算数据见表3。两种方法的可靠指标计算结果及失效概率见表4。
表1各随机变量分布参数取值情况
表2乘子法迭代计算数据
表3AFOSM法迭代计算数据
表4两种方法的可靠指标计算结果及失效概率
根据表2和表3可知,与可靠度指标β越大、失效概率Pf越小的一般规律相吻合。随着迭代过程的进行,可靠度与失效概率均逐渐趋于稳定,本文方法只需经过4次迭代即可得出结果,而AFOSM法则需要经过11次迭代才能得出结果。根据表4,使用本文方法和AFOSM法,最终都收敛于点(11.1855,1.6549),可靠度指标β=2.3302,失效概率Pf=0.0099。两种方法的可靠度指标和迭代次数之间的关系如图1所示。本文方法的目标函数收敛曲线如图2所示,目标函数等值线如图3所示,目标函数等值线局部放大图如图4所示。AFOSM法的目标函数曲线图如图5所示,目标函数等值线如图6所示,目标函数等值线局部放大图如图7所示。
图1迭代次数和可靠度之间的关系
图2乘子法目标函数曲线图
图3乘子法目标函数等值线
图4乘子法目标函数等值线局部放大图
从图1~图7中可看出,本文方法和AFOSM法在求解可靠度指标时都能得到稳定和有效的解,但本文算法很快收敛,且得到精度较高的解。总之,本文所提出的方法对于不确定结构可靠度优化设计问题具有较好的适用性。
图5AFOSM法目标函数曲线图
图6AFOSM法目标函数等值线
图7AFOSM法目标函数等值线局部放大图
2.2汽车侧碰分析
在交通事故中,汽车发生侧面碰撞时缓冲空间小,车体变形大。侧围结构侵入量、侵入速度和侵入形态等对乘员安全性具有较大影响,B柱最大侵入量是衡量汽车侧碰中耐撞性的重要指标。可移动障壁以50km/h的速度从侧面撞向汽车侧身,侧碰有限元模型如图8所示,车辆侧碰设计变量如图9所示,以汽车关键设计尺寸中左侧车体框架厚度x1、左前车门防撞梁厚度x2、左侧A柱内板厚度x3和外板厚度x4为设计变量,边缘BPA如表5所示,x1、x2、x3、x4相互独立[15]。
图8汽车侧碰有限元模型图9车辆侧碰设计变量
借助实验设计,运用拉丁超立方设计方法从设计空间中选28个样本点,调用有限元模型分析,构建最大侵入量b的响应面函数。B柱下端最大允许侵入量bmax=290mm,可建立如下极限状态方程:
列出以下3种参数取值,求解可靠度指标。
表5车身板厚边缘BPA
1)取第1组中各随机变量的均值为区间的中间值,BPA数值为标准差,具体的随机变量分布参数取值情况见表6。
表6各随机变量分布参数取值情况
根据本文方法,经过3次迭代,求得可靠度指标β=2.1421,失效概率Pf=0.0161,迭代计算数据见表7。使用AFOSM法检验,经过12次迭代,求得可靠度指标β=2.1421,失效概率Pf=0.0161,迭代计算数据见表8。两种方法的可靠指标计算结果及失效概率见表9。
表7乘子法迭代计算数据
表8AFOSM法迭代计算数据
表9两种方法的可靠指标计算结果及失效概率
根据表7和表8可知,可靠度指标β越大,失效概率Pf越小。随着迭代步数的增加,可靠度与失效概率均逐渐趋于稳定,乘子法只需经过3次迭代可得出结果,而AFOSM法则需要经过12次迭代得出结果。根据表9,本文方法和AFOSM法最终都收敛于点(1.0056,1.2250,1.2010,1.0304),可靠度指标β=2.1421,失效概率Pf=0.0161。可靠度指标和迭代次数之间的关系如图10所示。
2)取第2组中各随机变量的均值为区间的中间值,BPA数值为标准差,具体的随机变量分布参数取值情况见表10。
表10各随机变量分布参数取值情况
根据本文方法,经过3次迭代,求得可靠度指标β=0.1298,失效概率Pf=0.4484,迭代计算数据见表11。使用AFOSM法检验,经过3次迭代,求得可靠度指标β=0.1298,失效概率Pf=0.4484,迭代计算数据见表12。两种方法的可靠指标计算结果及失效概率见表13。
表11乘子法迭代计算数据
根据表11和表12可知,计算数据和可靠度指标β越大,失效概率Pf越小的一般规律相吻合。随着迭代步数的增加,可靠度与失效概率均逐渐趋于稳定,本文方法和AFOSM法都需要经过3次迭代得出结果。根据表13,采用本文方法和AFOSM法,最终都收敛于点(1.0658,1.3998,0.9873,1.0005),可靠度指标β=0.1298,失效概率Pf=0.4484,可靠度指标和迭代次数之间的关系如图11所示。
3)取第3组中各随机变量的均值为区间的中间值,BPA数值为标准差,具体的随机变量分布参数取值情况见表14。
根据本文方法,经过3次迭代,求得可靠度指标β=0.4721,失效概率Pf=0.3184,迭代计算数据见表15。使用AFOSM法检验,经过3次迭代,求得可靠度指标β=0.4721,失效概率Pf=0.3184,迭代计算数据见表16。两种方法的可靠指标计算结果及失效概率见表17。
根据表15和表16可知,计算数据和可靠度指标β越大、失效概率Pf越小的一般规律相吻合。随着迭代过程的进行,可靠度与失效概率均逐渐趋于稳定,乘子法和AFOSM法都需要经过3次迭代得出结果。根据表17,采用乘子法和AFOSM法,最终都收敛于点(0.9784,1.5517,1.1105,1.1257),可靠度指标β=0.4721,失效概率Pf=0.3184,可靠度指标和迭代次数之间的关系如图12所示。
表12AFOSM法迭代计算数据
表13两种方法的可靠度指标计算结果及失效概率
图10迭代次数与可靠度之间的关系
图11迭代次数与可靠度的关系
图12可靠度与迭代次数的关系
经过上述分析,汽车侧碰在该设计变量和侵入量前提下是比较安全的,比较了AFOSM法和本文方法,发现本文方法收敛较快并能得到较高精度的解。总之,本文所提出的方法在求解汽车侧碰结构可靠度优化设计问题时,能快速收敛且得到稳定和有效的解,具有较好的适用性。
表14各随机变量分布参数取值情况
表15乘子法迭代计算数据
表16AFOSM法迭代计算数据
表17两种方法的可靠度指标计算结果及失效概率
3、结论
本文针对具有一定非线性程度功能函数的可靠性分析问题,提出了一种基于乘子法的结构可靠性分析方法。该方法充分利用外函数求解非线性优化问题的优点,从乘子法的KT条件出发,快速求解追踪到最优点。数值算例和工程算例的计算结果表明,相对于AFOSM方法,本文所提出的方法对求解非线性程度较高的极限状态方程具有较好的收敛速率。同时,本文方法将来可应用于一些复杂工程问题结构的可靠度反问题中,还可以应用在串并联可靠性分析求解问题。
参考文献:
[1]姜潮,黄新萍,韩旭,等.含区间不确定性的结构时变可靠度分析方法[J].机械工程学报,2013,49(10):186-193.
[2]王博,郝鹏,田阔.加筋薄壳结构分析与优化设计研究进展[J].计算力学学报,2019,36(1):4-15.
[7]徐强,陈健云,李静,等.基于贝叶斯理论的大坝体系可靠度计算方法[J].大连理工大学学报,2011,51(1):84-89.
[8]黄逸群,林从谋,黄清祥,等.隧道型钢喷混凝土初期支护的可靠度计算方法及应用[J].华侨大学学报(自然科学版),2014,35(2):212-216.
[9]高东川,马志涛,高东忍,等.基于一次二阶矩理论中心点法的深部软岩巷道稳定性分析[J].山东科技大学学报(自然科学版),2013,32(6):7-12.
[10]肖宇峰.基于同构子网判定的结点不可靠网络可靠度计算方法[J].科技导报,2014,32(16):39-44.
[11]李怀龙,赵坪锐,刘志彬.CRTSⅡ型板式无砟轨道轨道板横向可靠度的计算方法研究[J].铁道建筑,2015(3):98-102.
[12]李奎,赵东平,路军富.深埋隧道素混凝土衬砌可靠度计算模型研究[J].铁道建筑,2014(7):38-42.
[13]王鹏,刘护林,邓华,等.基于应力-强度模型的DTECS-2设备可靠度计算方法研究[J].铁道学报,2017,39(3):71-74.
徐柳,王锬,杜义贤,刘晋玮,黄文超,王林军.一种基于乘子法的结构可靠性分析方法[J].机械工程师,2020(06):35-39+42.
基金:国家自然科学基金项目(51775308);水电机械设备设计与维护湖北省重点实验室开放基金项目(2019KJX12);三峡大学学位论文培优基金项目(2019SSPY046).
分享:

2020年5月28日,教育部印发《高等学校课程思政建设指导纲要》,全面推进高校课程思政建设。《纲要》指出,全面推进高校课程思政建设是深入贯彻习近平总书记关于教育的重要论述和全国教育大会精神、落实立德树人根本任务的战略举措,高校要深化教育教学改革,充分挖掘各类课程思想政治资源,发挥好每门课程的育人作用,全面提高人才培养质量。
2020-11-21
随着现代科学技术的飞速发展,运筹学相关研究日渐深入,应用范围日趋广泛,在军事领域中的作用也越来越重要。军事运筹学是应用数学和计算机等科学技术方法系统研究各类军事活动,并为决策优化提供理论和方法的军事学科,具有多学科综合交叉、注重实际应用、应用范围广、注重方案的最优性等特点。
2020-08-10
《运筹学》是一门把科学的方法应用于建立和求解数学模型,以便采取行动解决实际问题的科学。也就是运用科学的方法(如分析、试验、量化等)来决定如何最佳地运营和设计各种系统的一门学科。[1,2]运筹学也是一门综合性学科,其整合了数学、计算机及其其他相关科学内容,以期获得最优的结果做出最准确的决策。
2020-08-10
在全球能源消费日益增长的背景下,除了建造新的发电厂外,“需求响应”为缓解紧张的电力需求提供了一个经济有效的方法。在需求响应模式下,供电商在电力批发市场价格升高或系统可靠性受威胁时给电力用户发出电力价格变更信号或诱导性调整负荷通知,电力用户根据这些信号改变习惯用电模式,错峰用电,从而保障电网稳定,并抑制电价上升的短期行为。
2020-07-08
RGV是一种无人驾驶、能在固定轨道上自由运行的智能车。它根据指令来控制移动方向还有距离,具有一个机械手臂、两只机械手爪加一个物料的清洗槽,能够完成上下料及清洗物料等任务。2003年,Malmborg教授及其课题组首先提出自动小车存取系统,它主要包括轨道导引小车系统,通过RGVS小车进行货物存取。
2020-07-08
专利是知识产权的主要表达形式,在当今知识经济、科技引领的时代下,已成为企业发展和竞争的制高点。专利质量体系与企业的运营发展息息相关,企业传统的产品市场占有量发展模式逐步采用创新竞争模式。对于企业而言,专利是保护自身产品、防御对他人侵权的重要武器;是企业技术创新能力的证明;是企业规划开辟多源收入的重要手段。
2020-07-08
在工程设计中,材料不均匀、安装误差等问题的存在,往往会对结构性能造成各种影响甚至破坏。传统结构设计没有考虑施工过程中的不确定因素,而实际施工中载荷和材料性质等不断变化,这些不确定因素会使失效概率不断增大。为了确保产品的结构可靠性,有必要对不确定结构可靠度分析方法进行研究。
2020-07-08
“魔鬼在细节”。做好国际工程项目,要如履薄冰,因为往往一个细节的疏忽,就会导致项目成本大幅增加。做好一个项目,业主和承包商之间需要一种良好的合作氛围。对于承包商来说,不能过于计较一城一池的得失,该放弃的放弃,该争取的争取,最终会形成一个共赢的局面。
2020-07-08
依据《孙子兵法》对国家情报战略进行系统运筹,能够明确在国际情报对抗中的情报主体与情报客体的资源与结构,所面临的问题和所受的限制,指导国家情报工作有目的地进行“造形”与“治气”,创造情报主体的行动优势,取得情报对抗的胜利,为国家安全与发展保驾护航。
2020-07-08
自由粒子优化算法作为基于量子算法模型中的骨架模型,结构简洁,易于实现,通过对算法进行策略的改进,会使得算法的性能得到很好的提升。在自由粒子模型下的零势阱和谐振子模型下的高斯势阱的启发下,将优化问题中的目标函数进行势阱等效和泰勒近似实现量子模型下的转化,通过粒子在空间中的存在形式指导优化算法的寻优过程,实现量子模型的搜索机制。
2020-07-08
人气:3210

人气:2783

人气:2628

人气:2543

人气:1558
我要评论

期刊名称:运筹与管理
期刊人气:3023
主管单位:中国科学技术协会
主办单位:中国运筹学会
出版地方:安徽
专业分类:科学
国际刊号:1007-3221
国内刊号:34-1133/G3
邮发代号:16-191
创刊时间:1992年
发行周期:月刊
期刊开本:大16开
见刊时间:一年半以上


影响因子:0.553

影响因子:0.322

影响因子:0.352

影响因子:0.000

影响因子:0.000
您的论文已提交,我们会尽快联系您,请耐心等待!
你的密码已发送到您的邮箱,请查看!